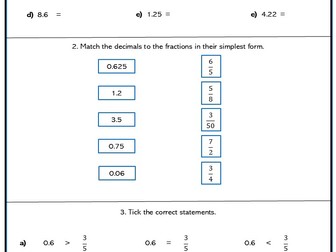
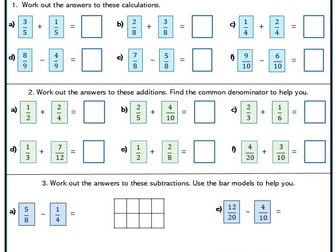
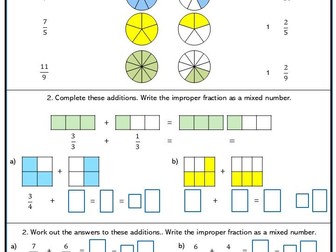
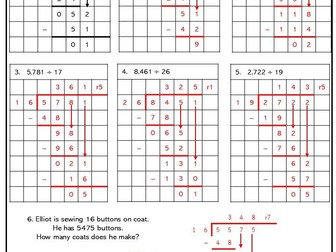
Ratio and Proportion Higher
<p>The worksheet is aimed at those working at greater depth.</p>
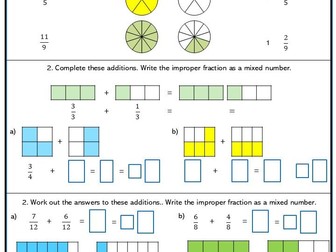
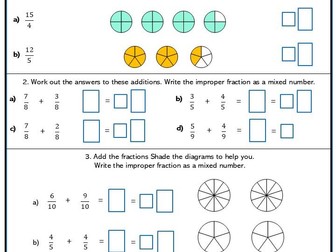
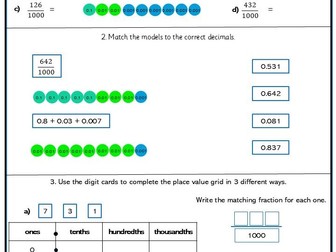
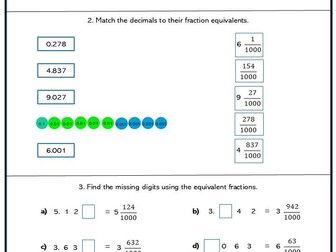
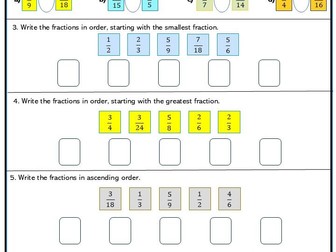
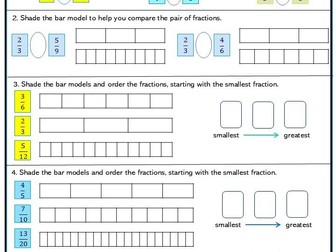
<p>Children divide numbers and quantities into a given ratio.<br />
They use proportional reasoning to solve problems.<br />
They solve percentage problems.</p>
<p>Answer sheet attached with detailed explanations.</p>