Graphs of Quadratic Functions (1)

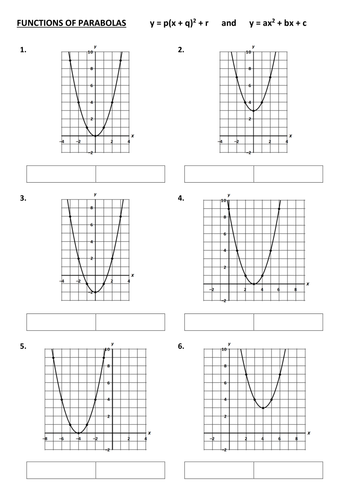
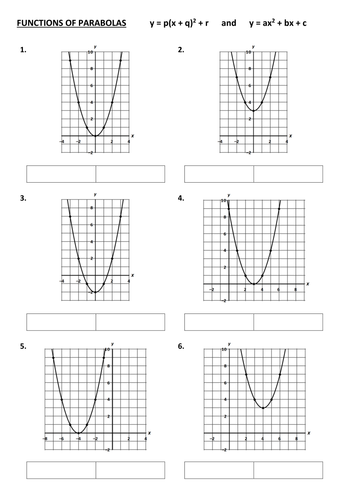
This worksheet has 30 parabolas drawn on individual coordinate systems. For each graph, the corresponding quadratic function needs to be found in the form of y = p(x + q)2 + r and then to be written in the form of y = ax2 + bx + c. The idea of this worksheet is to apply one or more transformations to the standard parabola with function y = x2 to find the functions of a range of parabolas. Transformations to be used are: horizontal translations, vertical translations, vertical stretches and reflections in the x-axis.
This worksheet is not only useful to introduce transformations of graphs and the effect they have on functions, it also provides practice for expanding brackets and shows the link between the two formats of quadratic functions as a first step towards completing the square. In ‘Graphs of Quadratic Functions (2)’ this link is further explored. The worksheet includes answers.
The worksheet is targeted at the full range of students (grades 4 - 9) doing GCSE Mathematics Higher Tier. It should take students, depending on their ability level and understanding of the topic, between one and two hours to complete this worksheet.

For your convenience, the Word file is included and can be edited to meet the needs of your students.