Circle theorems lesson 6

A complete lesson on the alternate segment theorem.

Assumes pupils can already use the theorems that:

1. The angle at the centre is twice the angle at the circumference
2. The angle in a semicircle is 90 degrees
3. Angles in the same same segment are equal
4. .Opposite angles in a cyclic quadrilateral sum to 180 degrees
5. A tangent is perpendicular to a radius
   so that more varied questions can be asked. Please see my other resources for lessons on these theorems.

Activities included:

Starter:
Some basic questions to check pupils know what the word subtend means.

Main:

• Animated slides to define what an alternate segment is.
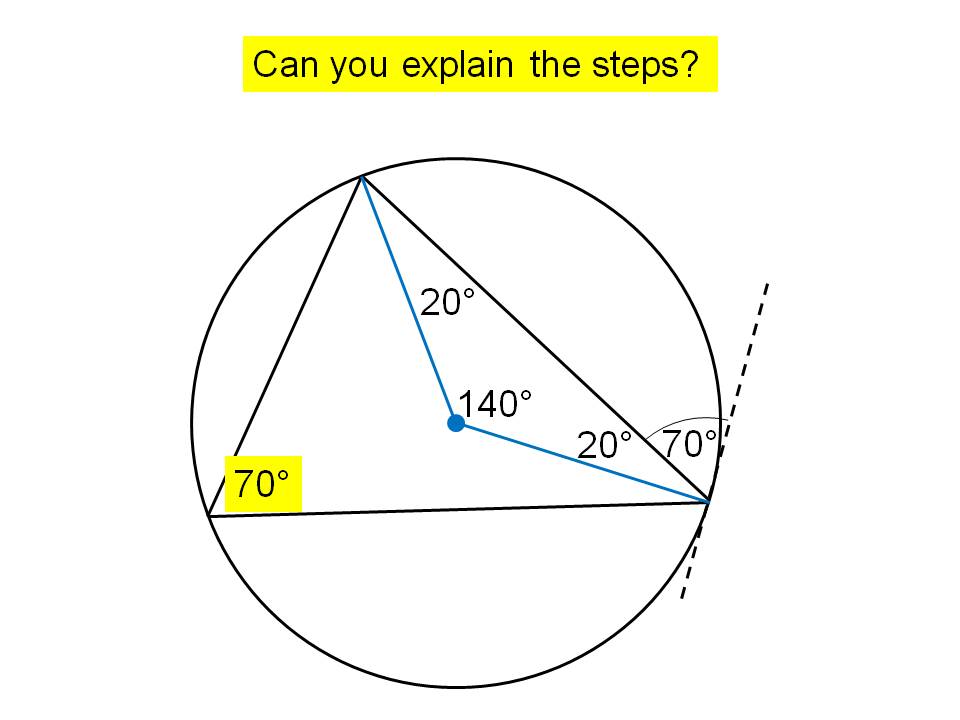
• An example where the angle in the alternate segment is found without reference to the theorem (see cover image), followed by three similar questions for pupils to try. I’ve done this because if pupils can follow these steps, they can prove the theorem.
  However this element of the lesson could be bypassed or used later, depending on the class.
• Multiple choice questions where pupils simply have to identify which angles match as a result of the theorem. In my experience, they always struggle to identify the correct angle, so these questions really help.
• Seven examples of finding missing angles using the theorem (plus a second theorem for most of them).
• A set of eight similar problems for pupils to consolidate.
• An extension with two variations -an angle chase of sorts.

Plenary:
An animation of the proof without words, the intention being that pupils try to describe the steps.

Printable worksheets and answers included.

Please review if you buy, as any feedback is appreciated.