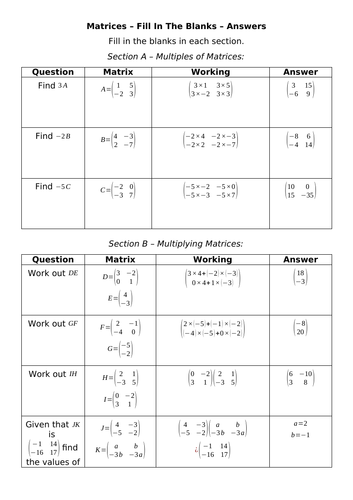
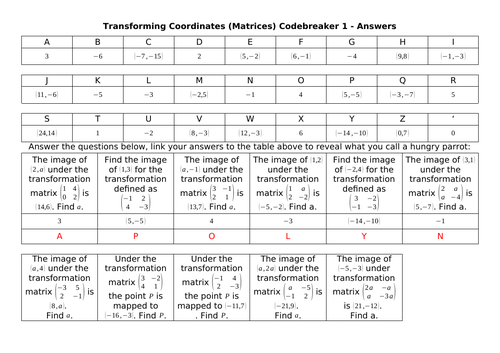
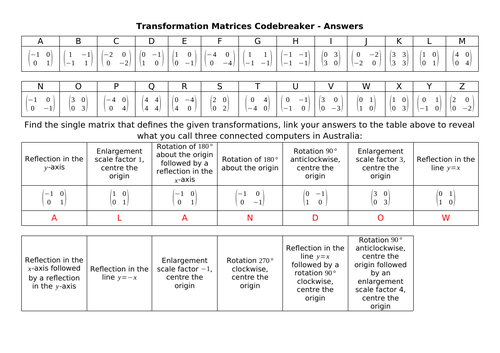
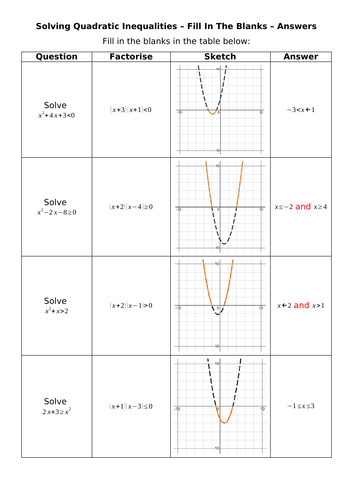
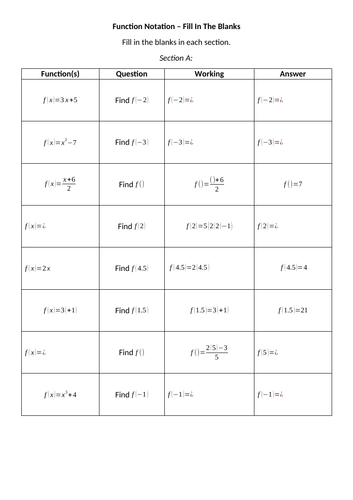
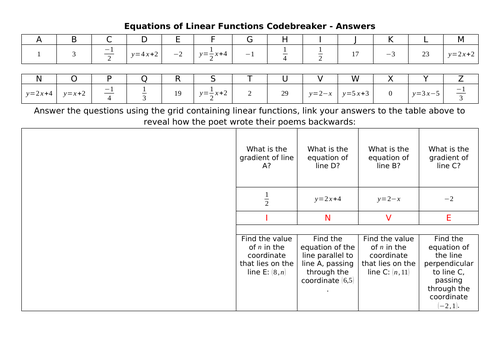
Andy Lutwyche's Shop
I have been a teacher for over 20 years - all the stuff I upload has been tried and tested in my classroom. I don't mind a discussion on Twitter too where I also share new resources. I now have a personal website: https://andylutwyche.com/