SUVAT Equations Application
<p>A dynamic resource which will make students think deeply about object moving freely under gravity.</p>
<p>You can use the Geogebra file to pratically create numerous versions of the same problem with different initial conditions and different results to interpret.</p>
Inverse Trigonometric Functions
<p>Wide range of questions on inverse trigonometric functions and their graphs.</p>
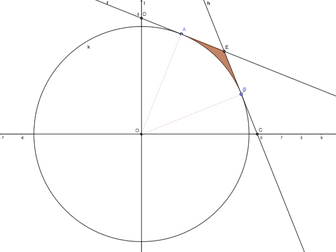
Inclined Plane Model
Inclined plane, friction, motion, forces
It is an interactive model of an object on an inclined plane. You can model various situations with or without friction and you can involve an additional force to act upon the object.
There is a slider called t that can animate how the object is moving 200m up or down the slope. If t -slider disappears when you change different variables like mass, coefficient of friction, angle of slope etc. that means the object cannot move due to a friction and if friction vector disappears that means the object will fly off.
MATHS GCSE_Level 9 and Above
<p>A collection of 24 questions for high achieving students designed to test their algebraic skills and use of proof to solve problems.</p>
<p>The questions are focused on algebra, algebraic proof, ratio and proportions and geometric proof.</p>
<p>You’ll get the questions and the full solutions in separate documents and together.</p>
Pie Chart Tamplate
Excel document with some simple pie chart templates, divided in equal pieces( 6,10,12,15,20) and some sets of date to be used with the templates
You can create your own template with as many pieces(slices) you want.
It works well with lower ability year 7 that are learning how to draw a pie chart..
undefined
Completing the square
A presentation about how to complete the square with the addition of a visual interpretation, worked examples and worksheets for students.
BEARINGS_Undersea rescue mission_Activity
Pair activity designed to test the accuracy of measuring and drawing bearings.
Solar System Modeling
A simplified model of the solar system with Venus, Mars, Earth and Jupiter.
If you want you can add all the other planets and moons. I didn't do it because of the computation limit of my PC.
You can discus on this model about measurements on large scale and the limitation of this model due to large numbers involved.
You can modify the numbers to mimic in a more precise manner the movement of the planets, the dimmensions of the planets and so on...
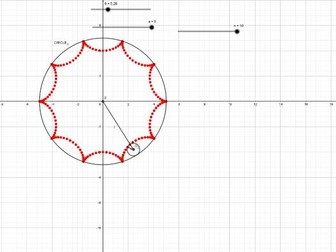
Parametric curves_The ASTROID
<p>An interactive way to see how a locus is generated through motion of other points and shapes.<br />
Also a nice example of parametric curves and how a computer can help visualising the dynamic component of parametric curves.</p>
Dodecagon_The new one pound coin
<p>A series of geometry problems related to the shape of the one pond coin. The images are from a maths blog and I thaught is something interesting to share with my students that will make maths more relevant to their every day life.</p>