Investigations using Pythagoras Theorem

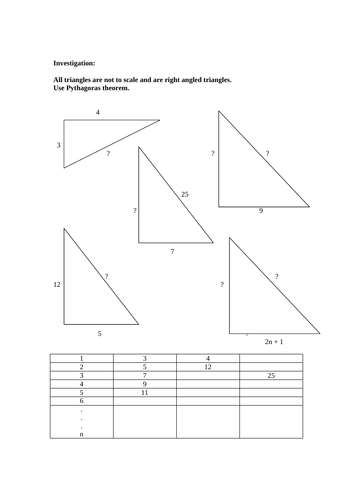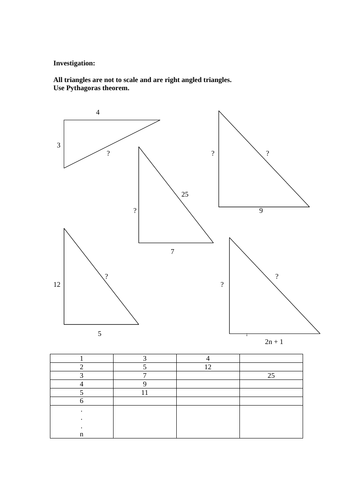
A sequence right angled triangles are presented. The smallest sides of the triangles are represented by odd integers - the smallest in this case chosen to be 3.

The challenge is when only one side (the smallest) is given and then finding the other two sides. It is expected the pupils to notice the other two lengths differ by 1. Then Pythagoras theorem is used to find the other two lengths.

For example, 4th pattern in the sequence, n is 4, so the smallest side is 9. Then, to find the other two lengths:

9^2 + x^2 = (x + 1)^2
81 + x^2 = x^2 + 2x + 1
81 = 2x + 1
2x = 80
x = 40

Filling column 2 is easy, but filling 4 and noticing the pattern of the sequence is a little challenging. In column 3 the following sequence should be found and factorised to notice triangular number sequence, whose generalisation is another challenge. The sequence in column 4 is: 4, 12, 24, 40, 60, 84 etc. This sequence can the be rewritten as: 4 x 1, 4 x 3, 4 x 6, 4 x 10, 4 x 15, 4 x 21 …
So now, it becomes obvious the sequence summarises to 4 x triangular number sequence, i.e., 4 x n(n+1)/2 = 2n(n + 1). The derivation of the triangular number sequence formula maybe left as exercise for pupils to establish.