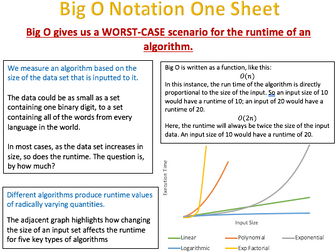
<p>A presentation comprehensively addressing the topic of Big O.</p> <p>The requirement for measuring algorithmic complexity is discussed along with multiple different metrics that could be employed to achieve this. Ultimately, the reasoning behind Big O is revealed and pupils guided as to why this metric is the most universally appropriate.</p> <p>Big O is comprehensively discussed, including how the data set size influences runtime and a range of different forms of Big O.</p> <p>This includes:</p> <ol> <li>Constant Time</li> <li>Linear Time</li> <li>Polynomial Time</li> <li>Exponential Time</li> <li>Factorial Exponential Time</li> <li>Logarithmic Time</li> </ol> <p>In each form, an example algorithm is provided to offer some context to the scenario. A visual representation of runtime with increasing data set sizes is also included for each, as is a visual comparison for each of the algorithms.</p> <p>Finally, the reason why Big O is important is addressed.</p> <p>There are 30 slides in this presentation, providing theory only. Exercises and run-throughs can be found in other uploads on my account.</p>

<p>A ‘one sheet’ document that covers all of the key aspects of Big O. Suitable for revision at A Level</p> <p>It assumes some understanding of the topic in advance of this resource being issued.</p> <p>Key aspects of the notation covered - constant time, linear time, polynomial time, exponential time, exponential factorial time, logarithmic time. Examples of algorithms are given for each aspect of the notation along with a description.</p>

<p>A short presentation highlighting some of the key forms of Big O.</p> <p>These include:</p> <ol> <li>Constant Time</li> <li>Linear Time</li> <li>Polynomial Time</li> <li>Exponential Time</li> <li>Factorial Exponential Time</li> <li>Logarithmic Time</li> </ol> <p>There is then a combined representation of each form, coupled with an explanation of Big O representing the worst-case for an algorithm.</p>