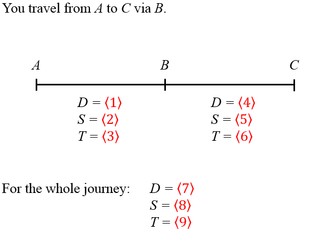
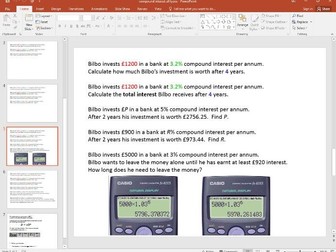
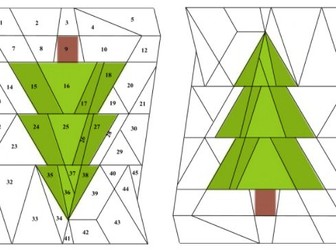
Similar Triangles Challenge/Extension Q
An old chestnut. Good as an extension or a challenge. I use it at the end of a lesson to see which pairs of similar triangles they can see (there are many). I find that many pupils correctly guess the height (2/3) but are unable to prove it. The steps in this PowerPoint should help.