

This is a free sample of my 93 slide PowerPoint presentation that covers all the content of A-Level Year 2 Differentiation. The notes pages for the full presentation are also provided.
We start with an introduction to connected rates of change using examples related to a sponsored charity walk. The examples provide students with an understanding that if one rate of changes leads on to a second rate of change then we obtain the overall rate of change by multiplying the two connected rates of change.
However, the foundation of Year 2 Differentiation is the Chain Rule, and how to use it to differentiate composite functions. Students struggle with the Chain Rule if they do not first have a solid grasp of composite functions. With this in mind, we remind students of how composite functions are created out of simpler functions.
We then provide an example of differentiating a function (a composite function) using our Year 1 method i.e. expanding brackets before differentiating. This example provides the opportunity to ask whether there is a quicker/simpler way of doing such a differentiation.
The term one-stage composite function is used for a composite function that can be differentiated without first having to simplify the expression. This leads to a two-stage composite function, and a proof of The Chain Rule.
Plenty of examples, and practice questions, are provided for the Chain Rule.
We then cover using the Chain Rule to prove that the rate of change of x on y is the reciprocal of the rate of change of y on x.
We next prove the Product and Quotient Rules, and provide various examples of combining them with the Chain Rule.
Next we expand the range of functions that we can differentiate from first principles, starting with trigonometric functions (small angle approximations are also covered).
Exponential functions are next, leading to the fundamental constant e, and the realisation that the gradient of the graph y=e^x at any point (x, y) equals the y-coordinate at that point.
A spreadsheet is provided so that trial and improvement can be used to guide students to the value of e.
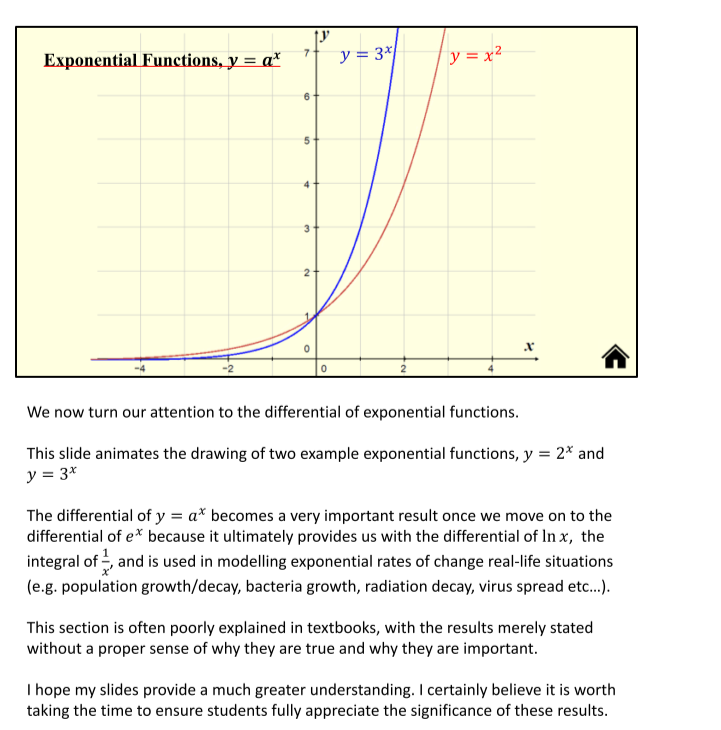
We next derive the differential of a^x and ln x.
This is a great opportunity to highlight this result as the missing piece from Year 1 differentiation i.e. we have now found the curve whose gradient is 1/x.
The next two sections provide further applications of the Chain Rule i.e. parametric equations and implicit differentiation.
The definitions of Concave, Convex and Point of Inflection are covered. The slide set goes further than the textbook, discussing the use of the 3rd differential.
The final section returns to where we began, namely Connected Rates of Change.
I hope you find the slide set useful in your teaching. I would be very pleased to receive any comments, or requests for improvements.
Regards
Gerard
Something went wrong, please try again later.
This resource hasn't been reviewed yet
To ensure quality for our reviews, only customers who have downloaded this resource can review it
Report this resourceto let us know if it violates our terms and conditions.
Our customer service team will review your report and will be in touch.