Gauss's formula

A complete lesson on the theme of the formula for 1+2+3+…+n, looking at how the rule emerges in different scenarios.

Activities included:

Starter:

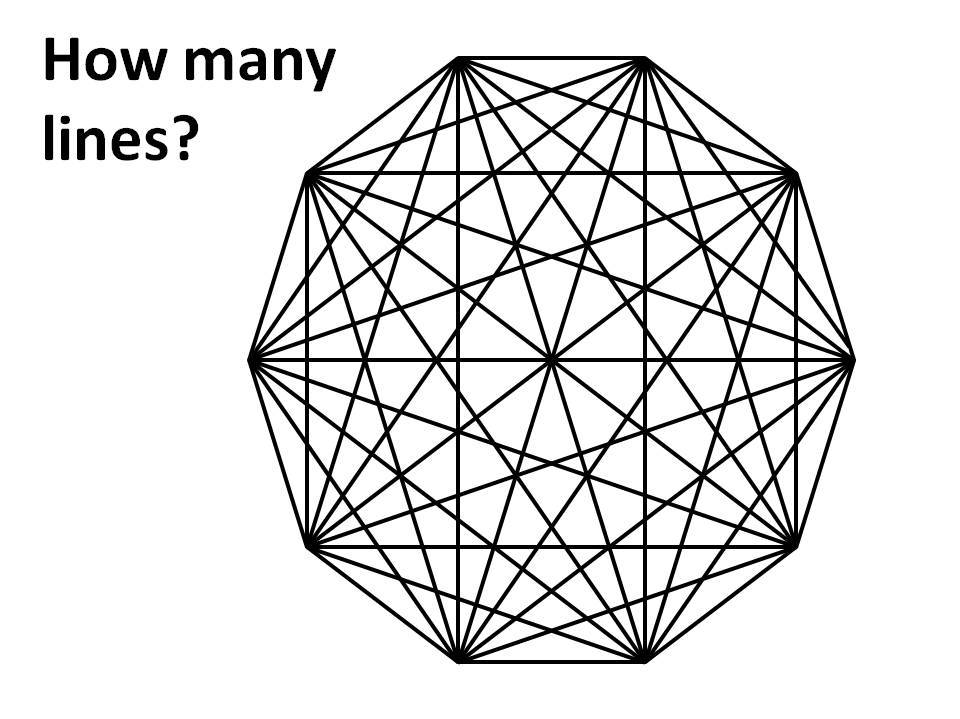
• A classic related puzzle - counting how many lines in a complete graph. After the initial prompt showing a decagon, two differing approaches to a solution are shown. These will help pupils make connections later in the lesson.
• This is followed by a prompt relating to the handshaking lemma, which is the same thing in a different guise. Pupils could investigate this in small groups.

Main:

• A prompt for pupils to consider the question supposedly put to Gauss as a child - to work out 1+2+3+…+100. Gauss’s method is then shown, at which point pupils could try the same method to sum to a different total.
• The method is then generalised to obtain Gauss’s rule of n(n+1)/2, followed by a worksheet of related questions. These include some challenging questions requiring pupils to adapt Gauss’s method (eg to work out 2+4+6+…+100).

Plenary:
A final look at the sequence Gauss’s rule generates (the triangle numbers).

Please review if you buy as any feedback is appreciated!