59Uploads
12k+Views
12k+Downloads
All resources

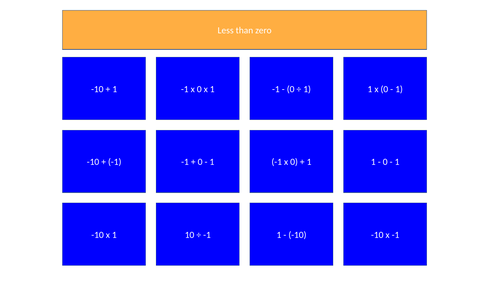
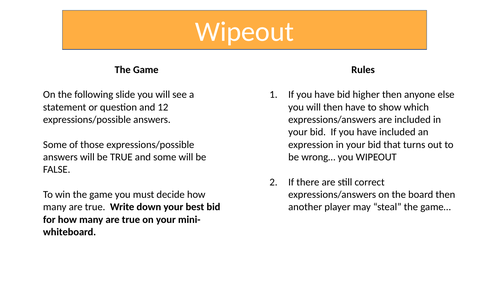
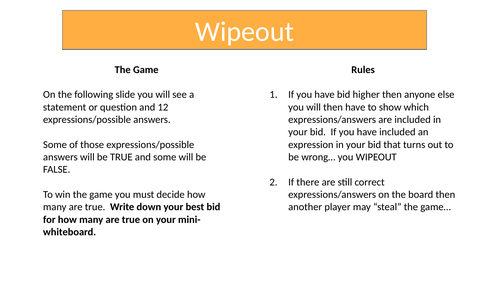
Wipeout - Less than Zero
Based on the old BBC quiz (with Bob Monkhouse). There are some expressions on the board that may (or may not) evaluate to less than zero. The objective is for students to ‘bid’ on how many expressions they can see that are definitely BELOW zero.
This activity is intended for use as a plenary - it relies on knowledge of the four operations in combination with directed numbers.

Dials - Equation of a Straight Line
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on understanding the gradient and y-intercept of a straight line stated algebraically.
Some of the clues require a student to identify which of the lines stated pass through a given point but none of the equations stated ever requires a student to expand brackets or to re-arrange equations.
My general concept for these dials is to provide a light revision activity but they may be of use in other contexts too.
Answers are provided in the powerpoint file (but this is not animated).

Dials - Algebraic Factors
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on factors and multiples of algebraic terms (with a few “clues” related to prime numbers and some related to square numbers).
The general idea behind these number dials is to provide a light revision activity but they may be useful in other situations. In particular I want students to begin to think about how to recognise whether an algebraic term is a square number and to contemplate what a multiple of an algebraic term can look like.
Answers are provided in the powerpoint file (this is not animated).
This worksheet follows on from the related (non-algebraic) worksheet:
https://www.tes.com/teaching-resource/resource-12538605

Wheels - Linear Equations between points
Turn the inner wheel to change the combinations of co-ordinates. Each combination of co-ordinates can be used to determine the equation of a straight line. Find the wheel setting that results in three straight lines that intersect at a single point.
I’ve made the resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present a rich problem solving activity for the topic in a visually novel format. There are a couple of extension questions for high ability students to consider.

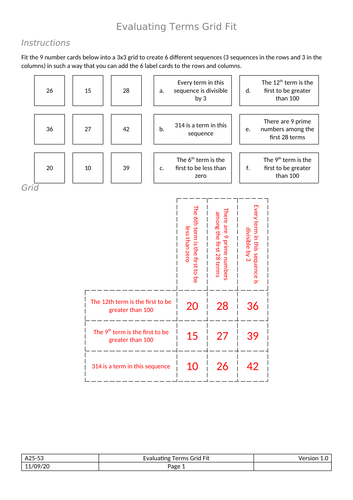
Grid Fit - Evaluating Terms of Sequences
Fit the numbers and labels into the grid to form 6 different arithmetic sequences that satisfy the labels.
This is designed as a problem solving task for students who have been taught how to evaluate whether a given value is a term within a sequence.

Capture the Squares Trigonometry
A series of ‘capture the squares’ games where the square value is the missing angle ABC. Angle ABC can often be determined by sketching the triangles and examining the sketch but it is intended that students use trigonometric ratios - specifically the task is intended to provide fluency work using the tangent ratio - to find the missing angle.
Can be used to consolidate learning or as bell work.

Capture the Squares - Coins
Capture the squares is a game intended for 2-3 players. Each takes turns drawing a horizontal or vertical line. When the fourth line around a square is drawn on the page, the player who placed that line takes the square.
Each square on this worksheet is a coin.

Capture the Squares Percentage of Amount
Capture the squares is a game intended for 2-3 players. Each takes turns drawing a horizontal or vertical line. When the fourth line around a square is drawn on the page, the player who placed that line takes the square.
Within each square there is a percentage of amount expression. The result of this expression is the value of the square taken (not all squares are of equal value).
The percentage of amounts in this particular game are designed to be calculated using a calculator. All amounts are integer but percentages are decimals. Percentages greater than 100% are included. All answers are decimals.

Algebraic Substitution - Wheels
Turn the inner wheel to change the value of variables to substitute into algebraic expressions. Find the wheel setting that results in the highest total value from the expressions.
I’ve made the resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present fluency practice for substitution in a visually more novel format.
There are a couple of suggested further extension activities for students to consider.

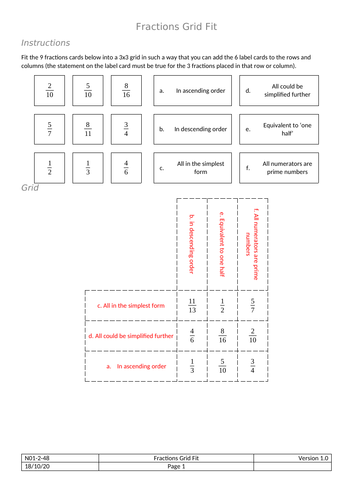
Grid Fit - Fractions
Fit the numbers and labels into the grid in such a way that the row/column labels satisfy all fractions within that row/column.
This is designed as a problem solving task for students who have been taught about comparing fractions and finding equivalent fractions.

Wipeout - Definitely NOT Prime Numbers
Based on the old BBC quiz (with Bob Monkhouse). There are some numbers on the board that MAY be prime numbers. The objective is for students to ‘bid’ on how many numbers they can see that are definitely NOT prime numbers.
This activity is intended for use as a plenary - it relies on knowledge of prime numbers but also tests students knowledge of some basic divisibility tests (all of the non-prime numbers can be divided by easily checked numbers like 3 or 4).
I’ve also included the slides in a “matching cards” format that can be cut out and given to students to sort into “true” or “false” on their desks (or in small groups).

Wheels - Surds
The inner and outer wheels each contain a value in surd format. Multiply the inner and outer numbers in each segment to find 3 different surds. Turn the inner wheel to change the combinations and find the wheel setting that results in all three segments multiplying together to give the same surd.
I’ve made each resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present a rich problem solving activity for the topic in a visually novel format.

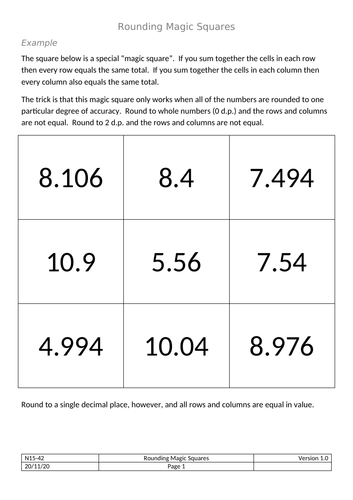
Rounding - Magic Squares
A couple of special “magic squares”* that are magic if - and ONLY if - all numbers within are rounded to one particular degree of accuracy.
Round the numbers to 1 d.p. and the square is NOT magic, round to 6 d.p. and the square is NOT magic - but round them to a particular accuracy and you will suddenly get a magic square.
*all rows and columns sum to the same value - but NOT diagonals

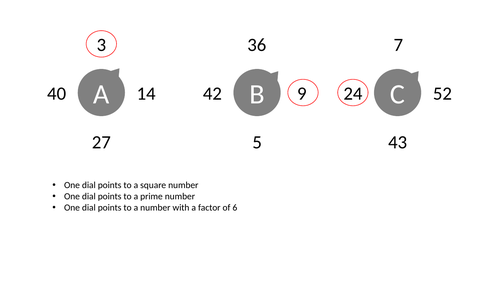
Dials - Factors
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”*.
This particular worksheet is focused on factors (with a few “clues” that require a student to distinguish between factors and multiples and some clues related to prime numbers).
The general idea behind these number dials is to provide a light revision activity but they may be useful in other situations.
Answers are provided in the powerpoint file (but this is not animated).
*I’m aware that with at least one of the groups I have introduced multiple possible correct configurations.

Dials - Values of Digits - Decimals
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on understanding the value of digits in decimal numbers.
Answers are provided in the powerpoint file (but this is not animated).

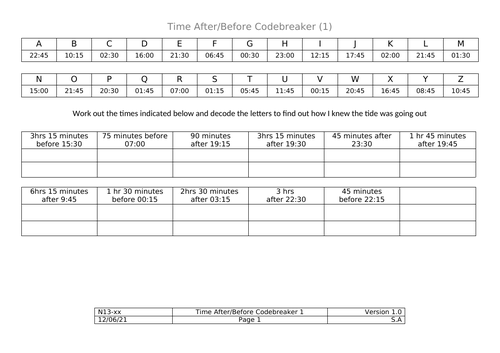
Codebreakers - Time After/Before
A couple of codebreakers in the popular format. Students should calculate the time described (always simple hours & minutes before/after a given time) to decode the answer to a bad joke.
There are 2 codebreakers - one that deals only in increments of 15 minutes and one that deals in increments of 5 minutes.
I had found plenty of other codebreakers on similar topics but not ones that did specifically what I wanted so hopefully these are of use.

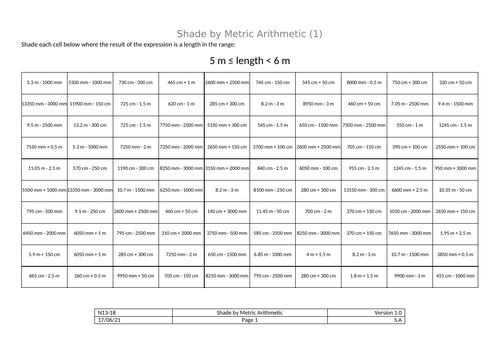
Shade by Metric (distance) Addition
Add or subtract lengths (given in different metric units) and assess whether the answer lies within a given range. Shade those cells that lie within the range.
All worksheets require students to work with a combination of mm, cm and m but the booklet gradually increases in difficulty as students progress.

Wipeout - Big Square Numbers
Based on the old BBC quiz (with Bob Monkhouse). There are some numbers on the board that are (large) square numbers and others that are not (these answers wipeout).
Designed for use as a starter activity or plenary.
This particular Wipeout is a good extension for KS3 students who already have secure basic knowledge of what square numbers are.
I’ve also included the slides in a “matching cards” format that can be cut out and given to students to sort into “true” or “false” on their desks (or in small groups).

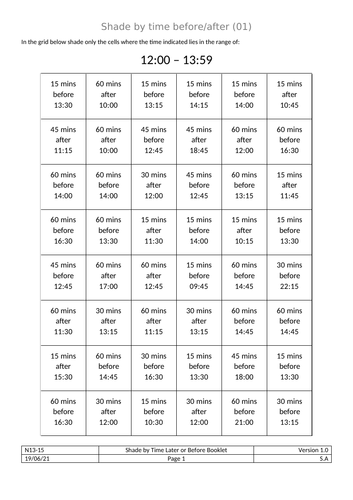
Shade by Time Later/Before
Each cell contains a description of a time (before or after a given time). If the time described fits within a given range then the cell should be shaded.
The booklet has 16 shade-by-time worksheets to complete - each one forms a simple pattern upon completion.
This is a good activity for students who need practice on the basics of arithmetic with time (which is a small but vital skill for both GCSE and Functional Skills).
The booklet gradually increases in difficulty in a number of ways as students progress through.