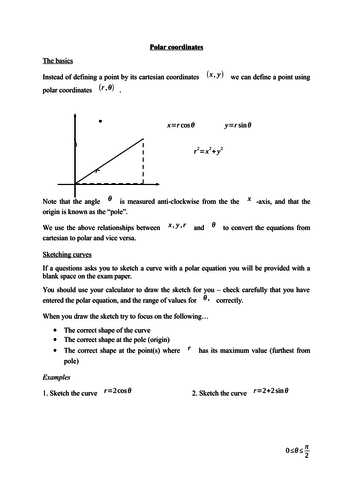
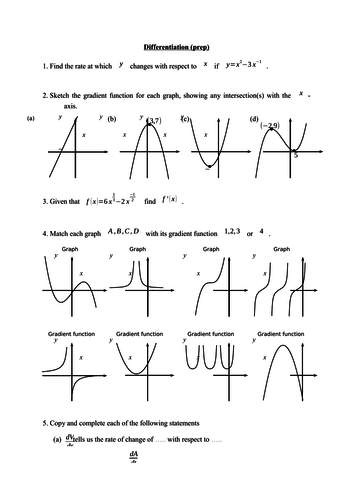
MathsWorksheetMaster's Shop
All my resources have been created to use with classes I teach. Often I've created resources because, for a particular topic, I haven't been happy with the number/standard of the examples in a textbook. Sometimes I've created worksheets for certain topics (e.g. graph transformations) because I feel my classes will make greater progress on a printed worksheet than trying to work from a textbook. I always aim to produce high-quality resources that improve the students' learning and understanding.