55Uploads
33k+Views
25k+Downloads
All resources

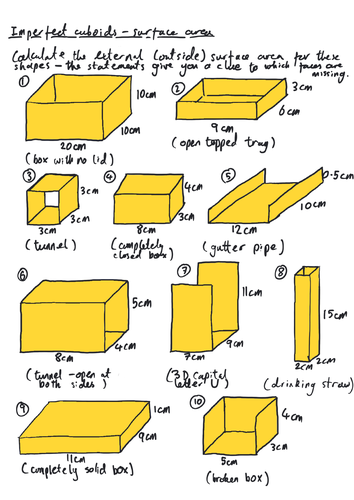
Cuboid surface area - incomplete and compound shapes
Some quick, hand drawn questions finding the surface area of “imperfect” cuboids (with holes in them or missing faces) and compound shapes. Numbers have been kept deliberately small to avoid pupils getting bogged down in number work, allowing them to focus on the actual shapes.

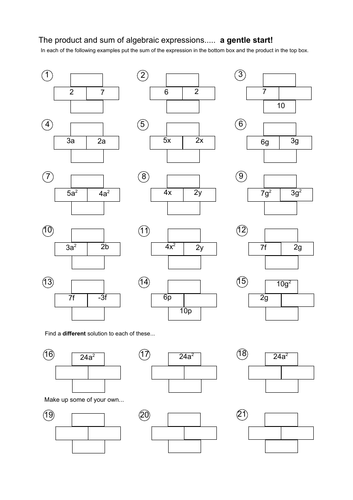
Product sum bricks
Pre-requisit for quadratic factorising - considering the sum and product of two terms. This task looks at integers and algebraic terms (with some extension into factorising). It’s in three levels - it’s designed for pupils to pick their own level rather than working through all the sections.

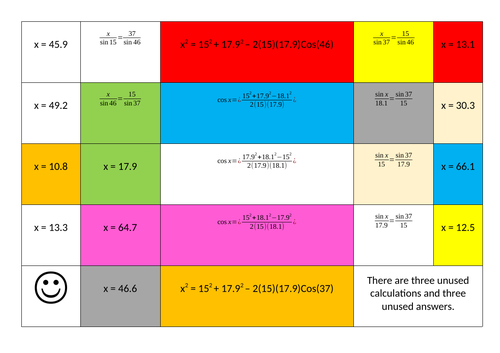
Non right angled trigonometry matching task
Eight triangles to match up with the appropriate trig rule and answer. Triangles repeatedly use the same numbers to keep students on their toes. There are three extra sets of workings which pupils can create their own triangles for.
Worksheet and answers as pdf and editable word.

Thinking about averages and spread using towers
This task focuses on what the averages look like rather than how to calculate them. This could be done with piles of blocks/cubes if you wish (though some of the means work out with decimal values).
Inspired by the “mean average equal sharing” activity by Don Steward:
Resources uploaded:
PDF of resource
Editable Excel spreadsheet of resource
Don Sterward slides from above link

Finding multiples of 10% using grids
Nothing fancy. Find multiples of 10% by finding 10% first. Scaffolded around a diagram of 100% split into ten equal boxes of 10%. Pupils fill in the value of 10% and shade in the required amount.
PDF and editable Excel file included.

Dienes Blocks and Percentages
A set of tasks using Dienes blocks to make connections with percentages.
I used it as a handout for the pupils. On reflection it might work better with the “information” bits being used as teacher notes then pupils trying the tasks in their jotters. The “information” could be used as teacher led examples on the whiteboard using the mathbot website while the pupils working through the tasks with the manipulatives and whiteboards to get the answers.
I worried too much about pupils recording their answers and methods which got in the way of them actually using the manipulatives. I’d recommend just leaving the pupils to use the blocks to get their answers and build an understanding first and then firm up the formal layout in later lessons.
I’ve included the resource as a PDF and a Word doc which you can edit as you see fit.

Solving linear equations - questions for use with algebra tiles
Some linear equations to solve when using algebra tiles.
The challenge when using tiles is the numbers getting too big and running out of tiles.
These questions keep the numbers deliberately small to minimise the amount of tiles each pupil requires.
Most of these are solvable with a maximum of 8 “x” tiles and 10 “1” tiles.
The solutions should all be integers.
I didn’t issue the sheet but used it as teacher notes and displayed the “your turn” on the white board when pupils were working independently.
I used the excellent MathsBot website to demonstrate on the white board: https://mathsbot.com/manipulatives/tiles

Trigonometric Equations - matching cards task
Pupils have to rearrange trig equations to solve. This is done by matching up cards from each column. Some cards have been deliberately left blank. Some common errors have been considered and included (ie 3 - 5tanx = 0 may be incorrectly matched up to the card tan x = 5/3).
Pupils could complete task by cutting and sticking down matched cards or labeling/colour coding the matching cards without cutting up.
Task in pdf form. Answers included as is an editable word doc version.
Task made for a National 5 (Scottish SQA) class.
Fixed version uploaded: 26/11/21

Solving Trigonometric Equations With Graphs
First handful of questions have pupils solving trigonometric equations by sketching graphs to identify which quadrants solutions lie in and using the symmetry of said graphs to find the value of these solutions. The second half of the task changes the problems to have pupils working back from a graph or solution to create the equations for themselves.
EDIT: There are a couple of errors on the last page of the answer file.

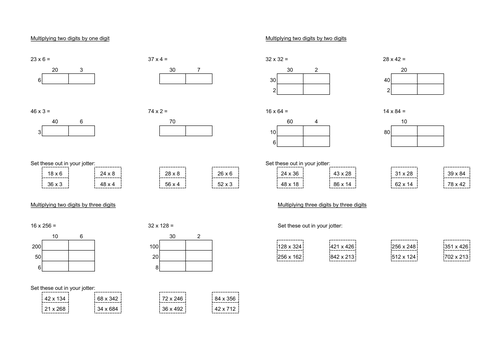
Multiplication with grids worksheet
Grid multiplication of:
2-by-1 digits
2-by-2 digits
2-by-3 digits
3-by-3 digits
Each section offers support in the form of predrawn grids. Level of support lessens with each grid. Pairs of questions have the same answer as a way for pupils to self check their work. These answers also offer the opportunity for discussing the effect of “double one, half the other”.

Completing the square and factorising using grids
A resource allowing pupils to use grids to complete the square and factorising trinomials. The first 5 questions are straight forwards enough but the ones following that have been deliberately picked to give deliberate results to facilitate discussion. Q6 gives the same result twice (ie it factorises to give a perfect square), Q7 and Q8 will not factorise (pupils will hopefully note these ones have a completed square constant that is not a square number), and Q9 is already in completed square form).
The second side of the sheet gives pupils different starting points - either the factorised form or completed square form for pupils to work backwards from. The last four questions give pupils a chance to think about what they have done and to create their own trinomials to meet give criteria.
Resource included as a pdf for ease of printing and an Excel file in case you wish to edit or adapt the resource for yourself.

Special numbers worksheet (square, triangular, Fibonacci, Pascal)
A set of tasks for pupils to pick and chose from working with square numbers, triangular numbers, Fibonacci numbers, and Pascal’s triangle.
Some made up by me, some from various sources credited in the pdf attached.

Straight line equation open questions
Pupils have to write appropriate equations for the lines on the axes.
Good for reinforcing what the terms gradient and y-intercept actually mean.
In some cases there are an infinite number of right answers and even more wrong answers!

Quadratics (solving equations and plotting) National 5 (N5) Mathematics
SMART Notebook file and pupil handout. Notes for teacher lead discussion and tasks for pupils to do within the notes.

N5 Trigonometric equations and identities
Smartboard files for use on an interactive whiteboard. PDF versions of the same file for printing as booklets and issuing to pupils. Notes contain examples for teachers to go over on the board and some tasks for pupils to do. Answers are included on the final pag or as pullout tabs at the side of the slide. Questions and examples have been sourced from various resources so make sure you’re not issuing the same task twice!
DISCLAIMER: There are most likely errors in here as I’m bad at proof reading my materials so read and check over before using!

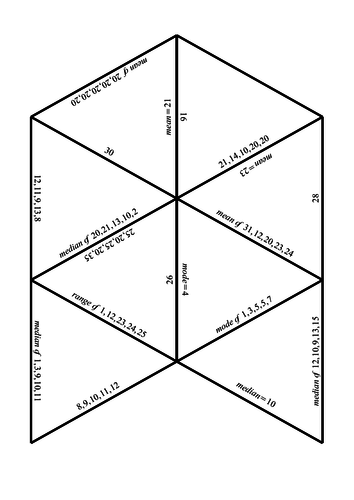
Averages and range jigsaw
Puzzle calculating mean, median, mode and range.
Some questions tell pupil what average to find (eg “mean of 20, 20, 10, 14, 16” matches up with the card “16”) where as some just give the list and pupils have to find all averages and range before matching up (eg “12,11,9,13,8” matches up with “median = 11”).
No repeated answers so there should only be one unique solution.
PDF of file included for those without the Tarsia software, original Tasia file included for those that want to edit the file.

Translating with vectors SPACE INVADERS
Using column vectors to move blocks around to create Space Invaders. Four problems in total - each one is a little bit more complicated than the one before it.
The worksheet should be free from errors but I’ve uploaded it as an editable Word file just in case! A scan of my solutions is also included.

National 5 (N5) Mathematics Surds and Indices
A Smart Notebook presentation and accompanying pupil booklet on the topic of Surds and Indices. Tasks for pupils to do throughout taken from a variety of sources (Don Stewrd’s Median blog: https://donsteward.blogspot.com/ and Dave Taylor’s Increasingly Difficult Questions: http://taylorda01.weebly.com/increasingly-difficult-questions.html in perticular).