59Uploads
12k+Views
12k+Downloads
All resources

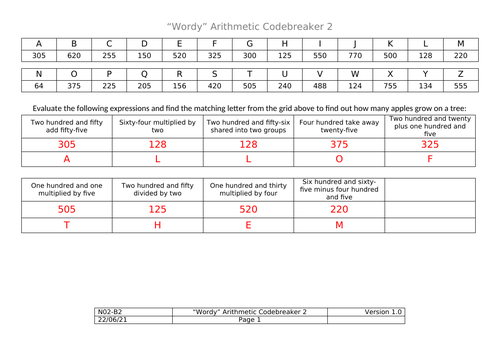
Codebreakers - Four Operations (in words)
A couple of codebreakers (in the format that seems very popular on TES) that I made for use with low ability yr 7 students built around completing simple arithmetic but with numbers presented as words instead of as numerals.
There are two codebreakers here - the second one is more difficult than the first.

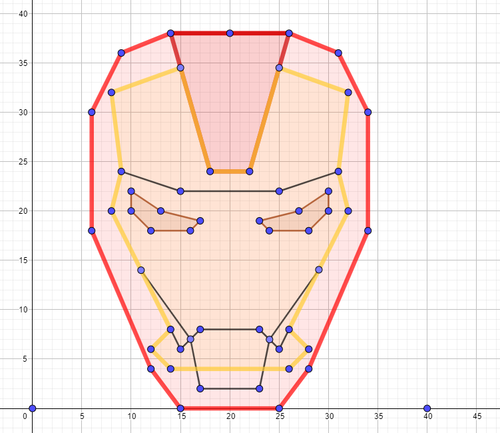
Plot Co-ordinates Superhero Picture
Plot the given co-ordinates to form an image of Ironman.
I’ve provided the same worksheet with 3 alternatives - one that forms the image entirely in the first quadrant, one that forms the image across the first and second quadrants and one that forms the image across all four quadrants.
This should allow for mild differentiation of the same activity.

Dials - Algebraic Factors
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on factors and multiples of algebraic terms (with a few “clues” related to prime numbers and some related to square numbers).
The general idea behind these number dials is to provide a light revision activity but they may be useful in other situations. In particular I want students to begin to think about how to recognise whether an algebraic term is a square number and to contemplate what a multiple of an algebraic term can look like.
Answers are provided in the powerpoint file (this is not animated).
This worksheet follows on from the related (non-algebraic) worksheet:
https://www.tes.com/teaching-resource/resource-12538605

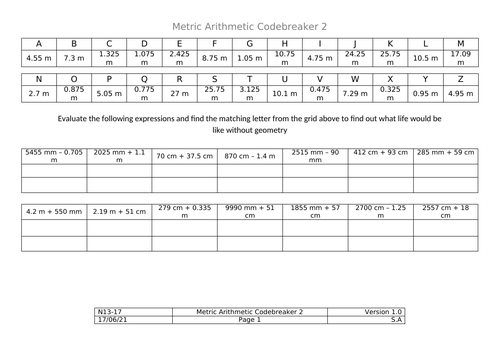
Codebreakers - Metric Length Addition & Subtraction
Codebreakers in the format popular on TES. These are focused on adding and subtracting lengths given in different units (e.g. mm + cm).
There are three codebreakers attached - each with a (bad) joke. They gradually become more difficult in various ways
Both codebreakers require students to convert units by multiplying/dividing by 10, 100 or 1000. The third is more challenging to decode (the units in the key for the first codebreaker are all in metres, this is not the case for the third).

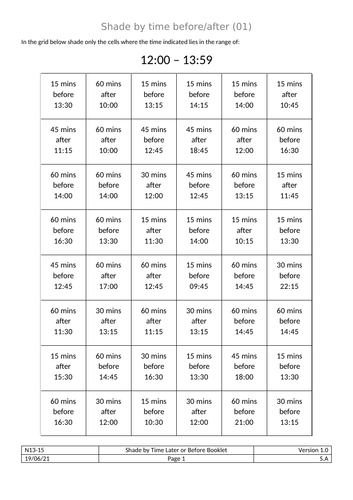
Shade by Time Later/Before
Each cell contains a description of a time (before or after a given time). If the time described fits within a given range then the cell should be shaded.
The booklet has 16 shade-by-time worksheets to complete - each one forms a simple pattern upon completion.
This is a good activity for students who need practice on the basics of arithmetic with time (which is a small but vital skill for both GCSE and Functional Skills).
The booklet gradually increases in difficulty in a number of ways as students progress through.

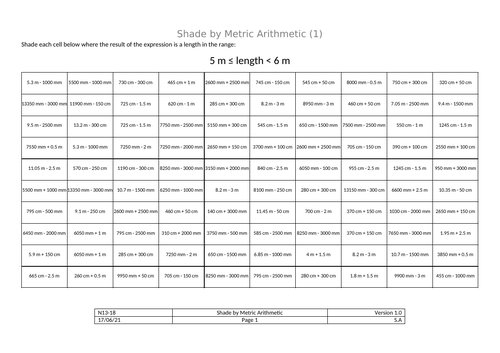
Shade by Metric (distance) Addition
Add or subtract lengths (given in different metric units) and assess whether the answer lies within a given range. Shade those cells that lie within the range.
All worksheets require students to work with a combination of mm, cm and m but the booklet gradually increases in difficulty as students progress.

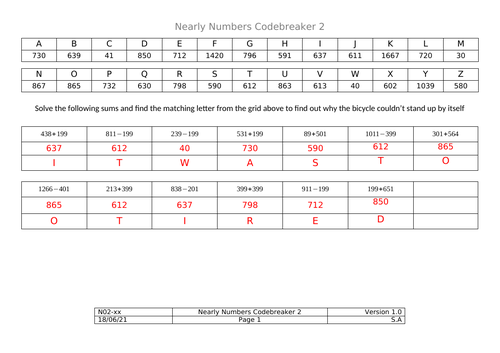
Codebreakers - Nearly Numbers Addition
A couple of codebreakers in the popular format. Students should solve the basic arithmetic to decode the answer to a bad joke.
There are 2 codebreakers - both involve the addition/subtraction of “nearly numbers” (that should ideally be rounded to the nearest 10 or 100 first before attempting arithmetic). The first codebreaker is relatively simple, the second is a slight step up in difficulty.
Both codebreakers are designed to be used with low ability groups to facilitate an understanding of place value.

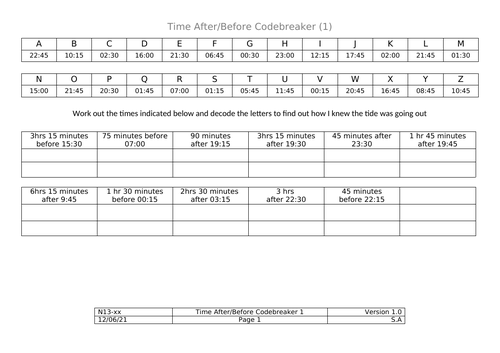
Codebreakers - Time After/Before
A couple of codebreakers in the popular format. Students should calculate the time described (always simple hours & minutes before/after a given time) to decode the answer to a bad joke.
There are 2 codebreakers - one that deals only in increments of 15 minutes and one that deals in increments of 5 minutes.
I had found plenty of other codebreakers on similar topics but not ones that did specifically what I wanted so hopefully these are of use.

Dials - Equation of a Straight Line
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on understanding the gradient and y-intercept of a straight line stated algebraically.
Some of the clues require a student to identify which of the lines stated pass through a given point but none of the equations stated ever requires a student to expand brackets or to re-arrange equations.
My general concept for these dials is to provide a light revision activity but they may be of use in other contexts too.
Answers are provided in the powerpoint file (but this is not animated).

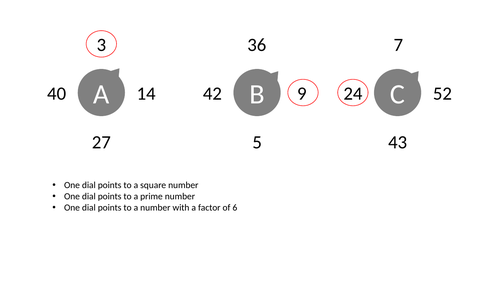
Dials - Factors
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”*.
This particular worksheet is focused on factors (with a few “clues” that require a student to distinguish between factors and multiples and some clues related to prime numbers).
The general idea behind these number dials is to provide a light revision activity but they may be useful in other situations.
Answers are provided in the powerpoint file (but this is not animated).
*I’m aware that with at least one of the groups I have introduced multiple possible correct configurations.

Dials - Values of Digits - Decimals
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on understanding the value of digits in decimal numbers.
Answers are provided in the powerpoint file (but this is not animated).

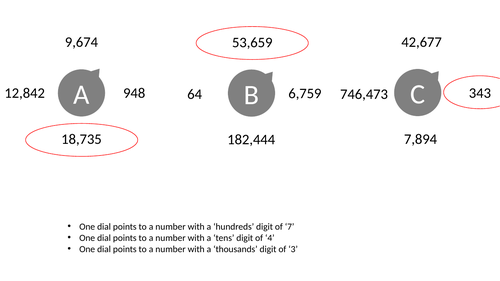
Dials - Values of Digits - Integers
Use the clues to set each dial to the correct answer. Often individual dials can be set to two or more possible settings but each group of three has only one correct “setting”.
This particular worksheet is focused on understanding the value of digits and includes questions in which the numbers are stated in words.
Answers are provided in the powerpoint file (but this is not animated).

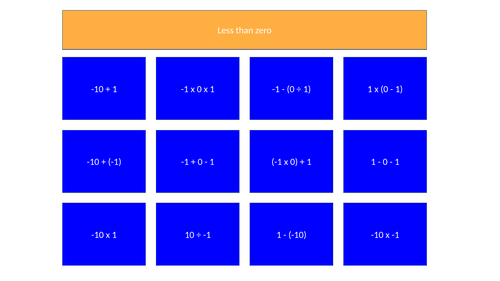
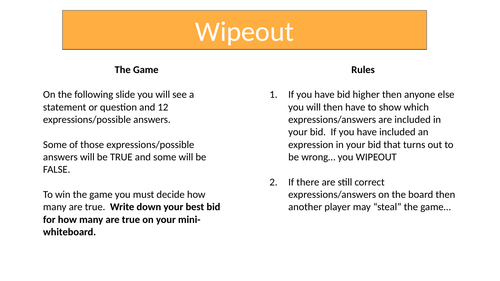
Wipeout - Less than Zero
Based on the old BBC quiz (with Bob Monkhouse). There are some expressions on the board that may (or may not) evaluate to less than zero. The objective is for students to ‘bid’ on how many expressions they can see that are definitely BELOW zero.
This activity is intended for use as a plenary - it relies on knowledge of the four operations in combination with directed numbers.

Shade by Equivalent Fractions Booklet
A 36 page booklet filled with equivalent fractions shading problems. Simply shade the cells that contain a fraction equivalent to the one listed at the top of the page to reveal an image.
There is a gradual increase in difficulty as the book progresses - all earlier pages require students to find equivalent fractions to simple unit fractions.

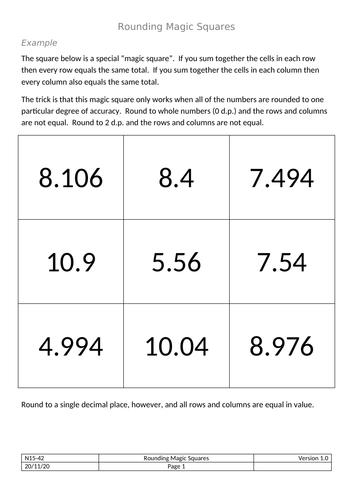
Rounding - Magic Squares
A couple of special “magic squares”* that are magic if - and ONLY if - all numbers within are rounded to one particular degree of accuracy.
Round the numbers to 1 d.p. and the square is NOT magic, round to 6 d.p. and the square is NOT magic - but round them to a particular accuracy and you will suddenly get a magic square.
*all rows and columns sum to the same value - but NOT diagonals

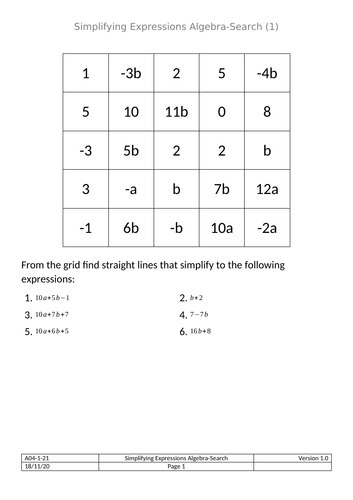
Collecting Like Terms - Algebra-search
A “wordsearch” that operates by collecting like terms. A series of expressions are given and the students must find a line (horizontal, vertical or diagonal) that simplifies to that expression when like terms are collected.
The resource includes a series of progressively more difficult grids to figure out.

Wheels - Surds
The inner and outer wheels each contain a value in surd format. Multiply the inner and outer numbers in each segment to find 3 different surds. Turn the inner wheel to change the combinations and find the wheel setting that results in all three segments multiplying together to give the same surd.
I’ve made each resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present a rich problem solving activity for the topic in a visually novel format.

Wheels - Simultaneous Equations
The inner and outer wheels combine to form 3 different equations. Turn the inner wheel to change the combinations and generate 3 different simultaneous equations in 2 variables. Find the wheel setting that solve consistently for the same values of a & b.
I’ve made each resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present a rich problem solving activity for the topic in a visually novel format.

Wipeout - Definitely NOT Prime Numbers
Based on the old BBC quiz (with Bob Monkhouse). There are some numbers on the board that MAY be prime numbers. The objective is for students to ‘bid’ on how many numbers they can see that are definitely NOT prime numbers.
This activity is intended for use as a plenary - it relies on knowledge of prime numbers but also tests students knowledge of some basic divisibility tests (all of the non-prime numbers can be divided by easily checked numbers like 3 or 4).
I’ve also included the slides in a “matching cards” format that can be cut out and given to students to sort into “true” or “false” on their desks (or in small groups).

Wheels - Solving Linear Equations
The inner and outer wheels combine to form 3 different equations. Turn the inner wheel to change the combinations and generate 3 different equations. Find the wheel setting that results in all three equations solving for the same value.
The first set of wheels are simple 2 step linear equations. The second set of wheels involve brackets. The third set of wheels includes variables on each side of the equation.
I’ve made each resource twice - once designed to be just printed and once where the inner wheels can be cut out and pinned to the outer wheels using paper fasteners (solutions can be found in the “cutting version”)
My main motivation in making this resource was to present a rich problem solving activity for the topic in a visually novel format. There are a couple of extension questions for high ability students to consider.