This 68 slide PowerPoint Presentation covers all the Mathematical Logic content required for TMUA Paper 2. It closely follows the content within the PDF resource provided by UAT UK. However, the PowerPoint slides build up in a way that makes the topic more easily understood (in my humble opinion). If you do not need to adapt the contents, you can download the associated PowerPoint Slideshow for free from TES. Regards and best wishes, Gerard

This 68 slide PowerPoint Slideshow covers all the Mathematical Logic content required for TMUA Paper 2. It is closely based upon the content within the PDF resource provided by the exam board. However, the PowerPoint slides build up in a way that makes the topic more easily understood (in my humble opinion). The slideshow is free to use as a teaching / leaner resource. If you which to adapt the contents to your teaching practice, you can download the associated PowerPoint Presentation for £5 from TES. Regards and best wishes, Gerard

This PowerPoint Presentation covers The Central Limit Theorem for Edexcel, A-Level Further Statistics 1, Chapter 5 The contents cover: The Central Limited Theorem in overview The general application of the Central Limit Theorem Applying the Central Limit Theorem to other distributions e.g. the Poisson Distribution and the Negative Binomial Distribution The presentation is fully editable for use as a teaching / learning aid in your own practice. If you do not want to adapt its contents, the associated PowerPoint Slideshow is available to download for free from TES. Regards and best wishes Gerard

The PowerPoint Slideshow covers The Central Limit Theorem for Edexcel, A-Level Further Statistics 1, Chapter 5 The contents cover: The Central Limited Theorem in overview The general application of the Central Limit Theorem Applying the Central Limit Theorem to other distributions e.g. the Poisson Distribution and the Negative Binomial Distribution This slideshow is free to use as a teaching / learning aid. If you want to adapt its contents to create your own teaching / leaning resource , the associated PowerPoint Presentation is available to download for £2 from TES. Regards and best wishes Gerard

This PowerPoint Presentation covers the Exponential Distribution with respect to A-Level Further Statistics. The topics coveed are; The connection between the Poisson and Exponential Distributions The formal definition of the Exponential Distribution The Probability Density Function (PDF) of the Exponential Distribution The Memoryless Property of the Exponential Distribution Finding probabilities using the PDF The median of the Exponential Distribution The IQR of the Exponential Distribution The Expected Value, E(X), of the Exponential Distribution The Standard Deviation of the Exponential Distribution You can fully adapt the presentation to your own teaching / learning requirements once you have downloaded it for £2. If you do not want to change its contents, the associated PowerPoint Slideshow is available to download for free from TES. Regards and best wishes Gerard

The PowerPoint Slideshow covers the Exponential Distribution for A-Level Further Mathematics. The contents cover: The connection between the Poisson and Exponential Distributions The formal definition of the Exponential Distribution The Probability Density Function (PDF) of the Exponential Distribution The Memoryless Property of the Exponential Distribution Finding Probabilities using the PDF The median of the Exponential Distribution The IQR of the Exponential Distribution The Expected Value, E(X), of the Exponential Distribution The Standard Deviation of the Exponential Distribution The slideshow is free to use as a teaching / learning aid. If you want to adapt its contents, the associated PowerPoint Presentation is available to download for £2 from TES. Regards and best wishes Gerard

The PowerPoint Presentation covers the contents of Chapter 4 of Edexcel’s Further Statistics 1 textbook. The contents cover: How the Poisson Distribution can be derived from the Binomial Distribution Formal Definition of the Poisson Distribution Alternative Derivation of the Poisson Distribution Modelling with the Poisson Distribution Adding Poisson Distributions The Mean and Variance of a Poisson Distribution Using the Poisson Distribution to model a Binomial Distribution This presentation can be adapted / amended to use as a teaching / learning aid. If you do not want to adapt its contents, the associated PowerPoint Slideshow is available to download for free from TES. Regards and best wishes Gerard

The PowerPoint Slideshow covers the contents of Chapter 4 of Edexcel’s Further Statistics 1 textbook. The contents cover: How the Poisson Distribution can be derived from the Binomial Distribution Formal Definition of the Poisson Distribution Alternative Derivation of the Poisson Distribution Modelling with the Poisson Distribution Adding Poisson Distributions The Mean and Variance of a Poisson Distribution Using the Poisson Distribution to model a Binomial Distribution This slideshow is free to use as a teaching / learning aid. If you want to adapt its contents, the associated PowerPoint Presentation is available to download for £2 from TES. Regards and best wishes Gerard

This PowerPoint Presentation covers the contents of chapter 4 (Hypothesis Testing) from Edexcel, Further Statistics 1. Topics covered: Hypothesis Testing and the Poisson Distribution Hypothesis Testing and the Geometric Distribution Critical Regions and Critical Values If you do not want to adapt the contents, you can download the associated PowerPoint Slideshow for free from TES. Regards and best wishes, Gerard

This PowerPoint Slideshow covers the contents of chapter 4 - " Hypothesis Testing" - from Edexcel, Further Statistics 1. Topics: Hypothesis Testing and the Poisson Distribution Hypothesis Testing and the Geometric Distribution Critical Regions and Critical Values This Slideshow is free. If you want to adapt the contents, you can download the associated PowerPoint Presentation for £2 from TES. Regards and best wishes, Gerard

This PowerPoint Presentation covers the contents of chapter 3 - " Geometric and Negative Binomial Distributions"- from Edexcel, Further Statistics 1. Topics: The Geometric Distribution The Mean and Variance of a Geometric Distribution The Negative Binomial Distribution The Mean and Variance of a Negative Binomial Distribution If you do not want to adapt the contents, you can download the associated PowerPoint Slideshow for free from TES. Regards and best wishes, Gerard

This PowerPoint Slideshow covers the contents of chapter 3 - " Geometric and Negative Binomial Distributions"- from Edexcel, Further Statistics 1. Topics include: The Geometric Distribution The Mean and Variance of a Geometric Distributuon The Negative Binomial Distribution The Mean and Variance of a Negative Binomial Distribution This Slideshow is free. If you want to adapt the contents, you can download the associated PowerPoint Presentation for £2 from TES. Regards and best wishes, Gerard

This PowerPoint Presentation covers the contents of chapter 3 - “Methods in Calculus” - from Edexcel, Core 2. Topics include: Improper Integrals The Mean Value of a Function The Mean Value and Graph Transformations Differentiation Inverse Functions (e.g. arcsin), and Associated Integrals Integration and Partial Fractions. You can adapt the contents to your own teaching. If you just want to use the slides without making any changes, you can download the associated PowerPoint Slideshow from TES free. Regards and best wishes, Gerard

This PowerPoint Slideshow covers the contents of chapter 3 - “Methods in Calculus” - from Edexcel, Core 2. Topics include: Improper Integrals The Mean Value of a Function The Mean Value and Graph Transformations Differentiation Inverse Functions (e.g. arcsin), and Associated Integrals Integration and Partial Fractions. This Slideshow is free. If you want to adapt the contents, you can download the associated PowerPoint Slideset for £2 from TES. Regards and best wishes, Gerard

This is a 93 slide PowerPoint presentation that covers all the content of A-Level Year 2 Differentiation. Full notes are provided for each slide, and a free preview presentation, containing approximately half the slides, is also available. We start with an introduction to connected rates of change using examples related to a sponsored charity walk. The examples provide students with an understanding that if one rate of changes leads on to a second rate of change then we obtain the overall rate of change by multiplying the two connected rates of change. However, the foundation of Year 2 Differentiation is the Chain Rule, and how to use it to differentiate composite functions. Students struggle with the Chain Rule if they do not first have a solid grasp of composite functions. With this in mind, we remind students of how composite functions are created out of simpler functions. We then provide an example of differentiating a function (a composite function) using our Year 1 method i.e. expanding brackets before differentiating. This example provides the opportunity to ask whether there is a quicker/simpler way of doing such a differentiation. The term one-stage composite function is used for a composite function that can be differentiated without first having to simplify the expression. This leads to a two-stage composite function, and a proof of The Chain Rule. Plenty of examples, and practice questions, are provided for the Chain Rule. We then cover using the Chain Rule to prove that the rate of change of x on y is the reciprocal of the rate of change of y on x. We next prove the Product and Quotient Rules, and provide various examples of combining them with the Chain Rule. Next we expand the range of functions that we can differentiate from first principles, starting with trigonometric functions (small angle approximations are also covered). Exponential functions are next, leading to the fundamental constant e, and the realisation that the gradient of the graph y=e^x at any point (x, y) equals the y-coordinate at that point. A spreadsheet is provided so that trial and improvement can be used to guide students to the value of e. We next derive the differential of a^x and ln⁡ x. This is a great opportunity to highlight this result as the missing piece from Year 1 differentiation i.e. we have now found the curve whose gradient is 1/x. The next two sections provide further applications of the Chain Rule i.e. parametric equations and implicit differentiation. The definitions of Concave, Convex and Point of Inflection are covered. The slide set goes further than the textbook, discussing the use of the 3rd differential. The final section returns to where we began, namely Connected Rates of Change. I hope you find the slide set useful in your teaching. I would be very pleased to receive any comments, or requests for improvements. Regards Gerard

This is a free sample of my 93 slide PowerPoint presentation that covers all the content of A-Level Year 2 Differentiation. The notes pages for the full presentation are also provided. We start with an introduction to connected rates of change using examples related to a sponsored charity walk. The examples provide students with an understanding that if one rate of changes leads on to a second rate of change then we obtain the overall rate of change by multiplying the two connected rates of change. However, the foundation of Year 2 Differentiation is the Chain Rule, and how to use it to differentiate composite functions. Students struggle with the Chain Rule if they do not first have a solid grasp of composite functions. With this in mind, we remind students of how composite functions are created out of simpler functions. We then provide an example of differentiating a function (a composite function) using our Year 1 method i.e. expanding brackets before differentiating. This example provides the opportunity to ask whether there is a quicker/simpler way of doing such a differentiation. The term one-stage composite function is used for a composite function that can be differentiated without first having to simplify the expression. This leads to a two-stage composite function, and a proof of The Chain Rule. Plenty of examples, and practice questions, are provided for the Chain Rule. We then cover using the Chain Rule to prove that the rate of change of x on y is the reciprocal of the rate of change of y on x. We next prove the Product and Quotient Rules, and provide various examples of combining them with the Chain Rule. Next we expand the range of functions that we can differentiate from first principles, starting with trigonometric functions (small angle approximations are also covered). Exponential functions are next, leading to the fundamental constant e, and the realisation that the gradient of the graph y=e^x at any point (x, y) equals the y-coordinate at that point. A spreadsheet is provided so that trial and improvement can be used to guide students to the value of e. We next derive the differential of a^x and ln⁡ x. This is a great opportunity to highlight this result as the missing piece from Year 1 differentiation i.e. we have now found the curve whose gradient is 1/x. The next two sections provide further applications of the Chain Rule i.e. parametric equations and implicit differentiation. The definitions of Concave, Convex and Point of Inflection are covered. The slide set goes further than the textbook, discussing the use of the 3rd differential. The final section returns to where we began, namely Connected Rates of Change. I hope you find the slide set useful in your teaching. I would be very pleased to receive any comments, or requests for improvements. Regards Gerard

This 34 slide PowerPoint presentation covers the contents of Edexcel FS1 Chapter 7 “Probability Generating Functions”. (I have also uploaded a free, 16 slide, preview presentation that shows you the level of detail contained within the slides, and the presentation style.) The presentation includes many new examples and proofs of the results covered within the topic. The full slide set also comes with my solutions to all the questions of every exercise (including the “Challenges”) within the chapter. (I do the questions independently from any published solutions, so you might find I have arrived at the same answer in a different way, showing detailed working along the way.) I am happy to receive any feedback you might have for further improvements to the presentation. Regards Gerard

This is a 16 slide, free preview of my 34 slide PowerPoint presentation covering Edexcel FS1 Chapter 7 “Probability Generating Functions”. This preview shows you the details contained within the slides, and the presentation style. I have included new examples and proofs of the results covered within the topic. The full slide set also comes with my solutions to all the questions of every exercise (including the “Challenges”) within the chapter. (I do the questions independently from any published solutions, so you might find I have arrived at the same answer in a different way, showing detailed working along the way.) I am happy to receive any feedback you might have for further improvements to the presentation. Regards Gerard

Chi-Squared Tests for Goodness of Fit This is a free preview PowerPoint slideshow, containing approximately half the slides, is also available. The full, 58 slide PowerPoint presentation covers the content of “Chi-squared Tests” within Edexcel Further Statistics 1 (Chapter 6 of the official Pearson FS1 textbook). Each slide is accompanied by teacher notes. We start with a general introduction for how you quantity the closeness of observed frequencies to the frequencies expected for a chosen standard distribution i.e. how to calculate Pearson’s Cumulative Test Statistic, X^2. Both methods of calculating X^2 are covered. In order to properly understand the concept of “Degrees of Freedom”, additional examples are included to fully explain how we determine the degrees of freedom of a given dataset by taking into account restrictions placed upon it. In my opinion, this is handled poorly by the textbook. The loss of degrees of freedom due to having to combine adjacent columns of the dataset (because the observed/expected frequencies are too low), and because the observed data itself is needed to calculated a required parameter of the model distribution is also covered. 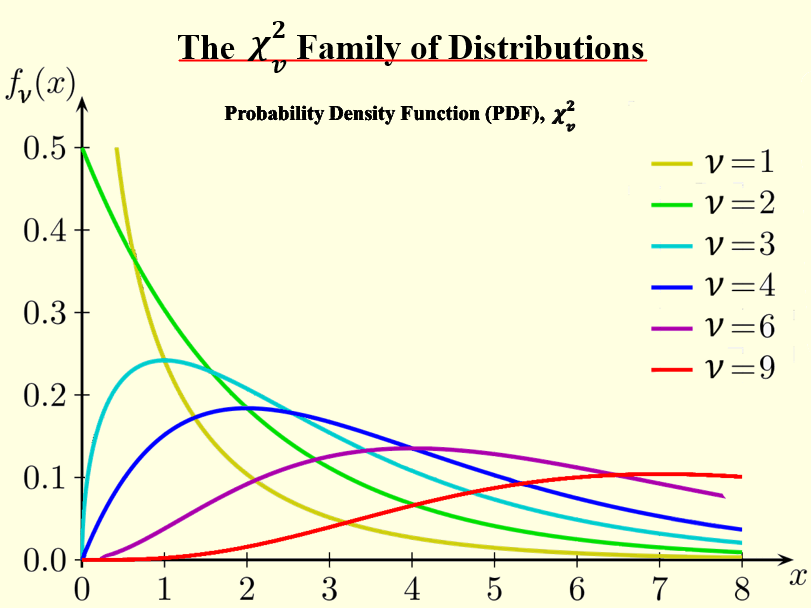We then link this to our existing knowledge of Hypothesis Tests, and introduce the Chi-squared family of distribution. This section has also been extended to ensure that students properly understand how the chi-squared graphs vary with the data’s degrees of freedom, ν, and how to effectively these graphs (either by using the table “Percentage Points of the Chi-Squared Distribution” in the formula book or by using a calculator e.g. the Casio CG50). Once we have the foundations in place, we use them to work through exam-style examples, comparing the given observed data to a chosen standard model distribution. For each example, we perform a hypothesis test to determine if there is sufficient evidence, at the required significance level, to reject null hypothesis. The examples cover the following standard distributions: Discrete Uniform Distribution Geometric Distribution Binomial Distribution Poisson Distribution All examples are either newly created or significantly modified from past paper questions. For each standard distribution we explain how to determine the probability of each outcome and, hence, the expected frequencies. We also explain how to, if necessary, estimate a required parameter (e.g. ρ for the Binomial distribution, λ for the Poisson Distribution) from the observed data. The presentation, unlike the textbook, deals with the four standard, discrete distributions in turn i.e. it does not delay the section on the Geometric Distribution until the end. Instead, the section on continency tables is left to the end and given its proper title of “The Chi-Squared Test of Independence”. In addition, the presentation contains detailed examples showing how to use the Casio CG50 calculator to perform Chi-Squared tests. Regards Gerard

Chi-Squared Tests for Goodness of Fit This 58 slide PowerPoint presentation covers the content of “Chi-squared Tests” within Edexcel Further Statistics 1 (Chapter 6 of the official Pearson FS1 textbook). Each slide is accompanied by teacher notes. [A free preview PowerPoint slideshow, containing approximately half the slides, is also available.] We start with a general introduction for how you quantity the closeness of observed frequencies to the frequencies expected for a chosen standard distribution i.e. how to calculate Pearson’s Cumulative Test Statistic, X^2. Both methods of calculating X^2 are covered. In order to properly understand the concept of “Degrees of Freedom”, additional examples are included to fully explain how we determine the degrees of freedom of a given dataset by taking into account restrictions placed upon it. In my opinion, this is handled poorly by the textbook. The loss of degrees of freedom due to having to combine adjacent columns of the dataset (because the observed/expected frequencies are too low), and because the observed data itself is needed to calculated a required parameter of the model distribution is also covered. We then link this to our existing knowledge of Hypothesis Tests, and introduce the Chi-squared family of distribution. This section has also been extended to ensure that students properly understand how the chi-squared graphs vary with the data’s degrees of freedom, ν, and how to effectively these graphs (either by using the table “Percentage Points of the Chi-Squared Distribution” in the formula book or by using a calculator e.g. the Casio CG50). Once we have the foundations in place, we use them to work through exam-style examples, comparing the given observed data to a chosen standard model distribution. For each example, we perform a hypothesis test to determine if there is sufficient evidence, at the required significance level, to reject null hypothesis. The examples cover the following standard distributions: Discrete Uniform Distribution Geometric Distribution Binomial Distribution Poisson Distribution _ All examples are either newly created or significantly modified from past paper questions. For each standard distribution we explain how to determine the probability of each outcome and, hence, the expected frequencies. We also explain how to, if necessary, estimate a required parameter (e.g. ρ for the Binomial distribution, λ for the Poisson Distribution) from the observed data. The presentation, unlike the textbook, deals with the four standard, discrete distributions in turn i.e. it does not delay the section on the Geometric Distribution until the end. Instead, the section on continency tables is left to the end and given its proper title of “The Chi-Squared Test of Independence”. In addition, the presentation contains detailed examples showing how to use the Casio CG50 calculator to perform Chi-Squared tests. Regards Gerard