46Uploads
42k+Views
17k+Downloads
Math

Algebraic expression into words
A matching activity where pupils need to match an algebraic expression e.g. xy into words e.g x multiplied by y.

Introducing and explaining column addition and its place value
This resource is designed for groups who are in the early stages of column addition. It is used a bit like a smartboard (although it's in word) as its examples need to be worked through with the children. Visually, the questions are shown with arrow cards to help show that adding 2 and 6 in the tens column is the same as adding 20 and 60. This also helps if you are then able to provide this resource children to use 'hands on' in the lesson. For questions that require carrying, the appropriate 10 or 100 is available at the bottom of the page to drag up in to the questions. The first questions are TU + TU with no carrying, reaching HTU + HTU with carrying by the end.

Maths competition quiz for KS2 Year 6 SATs revison
This quiz is ideal for two teams of between 4 and 8 but could probably be played with larger groups. It has four rounds including a buzzer round and speed round. There are questions that require team work and some that rely on every member of the team individually. Questions focus mainly on topics that come on the arithmetic paper but also on volume, area and angles.
Enjoy!
Edit: The first version I put online had a couple of simple errors which have now been corrected for future downloads. Apologies to anyone who was using it before I noticed the problem.
Also, I have noticed that it might be worth the teacher printing out the slides if you want the answers before revealing them on the projector (e.g. in the rounds where teams can steal points from each other).

Shapes and co-ordinates from equations of lines
This resource provides pupils with equations of lines (e.g. y = 8, y = 4...) that will form a basic shape on a grid. Questions then ask for the perimeter of the shape or the co-ordinates at the centre of the shape. It is good to encourage pupils to find a way of answering these questions without drawing accurate graphs every time but perhaps just little sketches or by looking at the appropriate numbers.
The fourth and final question uses the equations of straight lines to form a triangle with questions asking about the type of triangle and a new co-ordinate if the shape were reflected in the axis.

Fractions problem solving
Based on a GCSE exam question, this worksheet has four examples of tables that need filling in. Answers are provided and a helpful hints box at the bottom helps pupils to get started if needed.

Doing and undoing (algebra, proportions and fractions)
If I have six sweets and increase them by a half, what fraction would I have to reduce the result by to get back to the original 6 sweets?
This resource was made as a way of explaining a KS3 exam question I found, which used this idea but with x amount of sweets.

What algebraic expressions mean
This is a good resource for pupils beginning in algebra, especially those who like to know exactly what's going on and why. The left hand column of the resource gives written examples showing that, for example, 3 x a x a can be written as 3a(squared). It proves this by working the same example through with numbers. 3 x 4 x 4 = 3 x 4(squared) = 48.
The right hand column requires the pupil to have a go at writing a simplified algebraic expression based on the pattern in the left column. There is room to do a 'numbers version' if that helps.
At the bottom, there is a challenge to work the idea backwards, expanding expressions such as 6fg to find out what's really going on inside that expression.

Algebra Basics Bingo
These three games are a good introduction to algebraic terms and expressions and are designed for two players.
In two of the games, the question cards will have something like b + b + a + a and the players need to see if they have the simplified answer 2b + 2a on their grid.
In the third game, the question card might show yz + z and the pupil needs to expand it to y x z + z to see if they have it on their grid.

Addition and subtraction with negative numbers in the context of temperature
Here we have three resources. The first is a number line from -20 to +20 which will help pupils to complete the two activities.
The first activity asks pupils to increase or decrease a temperature by a given amount of degrees. Blue and red are used to help colour co-ordinate the questions depending on whether the temperature rises or drops. Later questions involve a temperature that first goes up and then comes down a bit, providing a basic two-stage question.
The second activity requires the pupils to do multiple increases or decreases (or both) to get a final temperature. For example: It's 11 degrees and the temperature drops by 2 degrees every night for six nights. It them increases by 3 degrees for one further night. What's the final temperature?

Making and proving statements using shapes and properties of shapes
The main activity in this lesson begins with asking children to make some true statements about a group of shapes (where the statement will be true for ALL shapes in that group).
From here the activity moves on to looking at a statement about a shape and seeing if children can find an example of a shape which proves this statement and another shape that disproves the statement. A sheet of shapes has been provided so children don't always have to draw shapes but can cut and stick instead.
This resource also comes with 3 introduction or follow up activities linked to shapes and their properties. There are instructions for drawing shapes with given properties; a Carroll diagram for sorting right angles and curved sides, and a table looking for the basic sides and corners of well-known 2D shapes.

Number bonds to 100
Four sheets are provided here: two classwork sheets and two homework sheets with a set for more able and a set for less able.
The sheets look first at making 100 using deines cubes, where children are encouraged to draw the extra cubes and sticks until they reach 100. The second half builds on this, making the link with the deines equipment that the cubes will always make a ten and the sticks will need to add up to the other ninety.
The homework sheets provide more practice of what has been covered in lesson.

Converting measure using lining up place value (rather than x/10,100,1000)
I made this resource when working with some weaker Year 6s who got in a massive muddle with converting cm, m and km. They couldn’t remember what to times and divide by, whether they were shifting the digits or decimal point (because different teachers had taught them differently!) or which way they were shifting things.
So this powerpoint/lesson avoids that method and uses the lining up method where they need to write down the conversion, then the question underneath and spot where 0s and decimal points need to go. E.g.:
1000m = 1.000km
0751m = 0.751km
The lesson starts with some warming up of place value and lining up decimal numbers.
It then moves on to look at units of measure and asks children to estimate some lengths, weights and volumes. (It seemed that my group had no idea what a ‘reasonable’ answer was, as they had no context of distance or weight.)
The powerpoint explains how to line up to find the answer.
Questions are provided and slides 26-29 should be printed for the independent worksheet.
All answers provided.
I appreciate children need to know the multiplying and dividing method for converting measure (see my other resources). This was a much-needed ‘quick-fix’ for SATs preparation. Please do make sure you go over the standard method with your class at a later date!

Properties of 3D shapes investigation - pyramids and prisms
This four page booklet begins with an explanation of the terms ‘edges’, ‘faces’ and ‘vertices’ and then tests this knowledge using three basic 3D shapes. The inside of the booklet has two tables and images of prisms and pyramids. It requires the pupil to find the number of edges, faces and vertices for ten of these shapes. It also asks them for the number of sides of the base shape on the pyramid and the number of sides of the cross-sectional shape on the prism. This is to help with the investigation on the final page. The last page asks pupils to look at the numbers in the tables and spot patterns/rules. It encourages them to express their thoughts in algebra if possible. Then, to test their theories, there are another two shapes to work with on this final page.
Aimed at Year 6 - Year 9 pupils.

KS2 Maths daily warm ups, starters, mental orals
Suitable for upper KS2, these powerpoints each contain 10 slides: half with questions and half with answers. Each slide has an activity that is differentiated but easily edited to suit your needs. My recommendation would be to let the children choose which colour box to start on and, if they finish ahead of time, they can progress onto the next box.
This resource is ideal for revision of recently covered topics or for 'just keeping things ticking over'.
Week 1: Number
Week 2: Calculation

Maths SATs Year 6 KS2 Arithmetic Revision Quiz
Use this with a small group or a whole class to revise some of the basic skills on the KS2 SATs Maths Paper 1: Arithmetic.
It is designed to be a quiz quick that more able pupils should be able to do in their heads and less able pupils should be able to do in a reasonable amount of time on a whiteboard. The questions are in a fairly random order, although I have often made 3 or 4 consecutive questions follow the same topic so the children get a chance to practise and get into a topic before the next topic comes along. I have also subtly colour-coded the questions so the teacher can instantly see the level of difficulty: 3 shades of blue, with the lightest representing easier questions and the darker shade representing the hardest questions. (This shading is just a rough idea - you may disagree with paritcular questions and want to change the shade! Also note that the shading is relative within the topic: the hardest of the x1000 questions is still much easier than finding 87% of a number!)
This resource could be used so flexibly as a gap-filler e.g. when you’ve got a spare few minutes at the end of the day or before assembly, as a lesson where you can try questions and then discuss mental methods across the class, or as a competitive quiz with teams or individuals, buzzer rounds and speed rounds. It can be saved for year after year too!
There are approx 200 questions covering the following topics:
adding and subtracting TU and TU: 26 + 63 and 53 – 21
adding on a multiple of 10, 100 and 1000: 3852 + 20 and 4284 + 3000
multiplying multiples of 10, 100 and 1000: 30 x 400
dividing multiples of 10, 100 and 1000: 450 ÷ 9
adding and subtracting decimals: 1 – 0.43 and 2 + 0.67
adding and subtracting 99
x ÷ 10 100 1000
x ÷ fractions
% of numbers
fractions of numbers
32 + 10
BODMAS
Answers included on a separate powerpoint. I have checked them but please let me know if you find any errors so I can amend immediately.

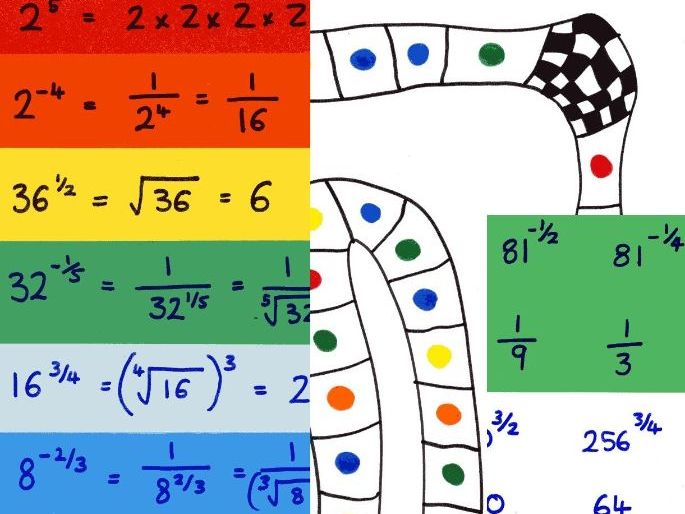
Fractional and negative indices matching cards and board game
I used this resource over two lessons.
In the first lesson we used the colour coded question cards to teach indices with increasing degrees of difficulty. The cards are coloured red, orange, yellow, green, blue and dark blue. With red having positive integer indices and orange having negative integer indices. As it works down through the colours, it introduces 1/2, -1/2, 3/4 and -3/4. There are five questions in each colour and the answers are available if you want to do it more as a matching exercise.
In the second lesson, I provided pupils with the prompt sheet of the 6 processes covered last lesson. With this as support (no exercise books allowed), we used the same question cards again to complete a board game in pairs. Instructions for the game are included, with suggestions for differentiation too. It went down very well, hence listing it here.