Place value is fundamental to our number system. It’s the key to fluency and efficiency in calculations; if you have a good understanding of place value, then you can make the numbers work for you.

However, place value is not a single concept: it is a complex combination of quite abstract ideas, which need to be carefully constructed, from early years foundation stage (EYFS) all the way through to Year 6.

Let’s take this seemingly simple key stage 2 Sats assessment question:

To answer this effectively, pupils will need to have a deep understanding of place value. But how do we help children to develop this?

According to the Department for Education, consistent use of the same manipulatives and representations across the year groups can be a huge help.

Here’s what that might look like in practice.

EYFS: Making sense of number

In Reception, children develop key skills in counting objects such as balls, cubes, toys and pieces of fruit at snack time - including saying the numbers in order and matching one number name to each item.

They develop an understanding that the cardinal value of a number refers to the quantity, or “howmanyness”, of things it represents.

The Education Endowment Foundation (EEF) explains that, at this point, it is important to expose children to different representations of number and then help them to make connections between them in order to support a fuller understanding. For example, understanding that the numeral 5, five spots on a dice face, five counters and a five-step on a number line all represent aspects of “five”.

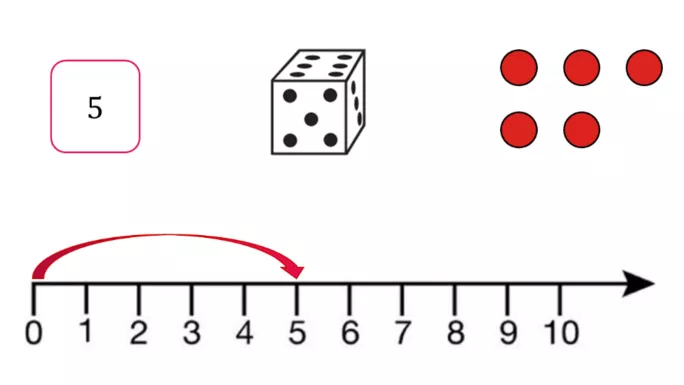
A range of visual models of numbers should also be used when children explore the composition of numbers to 10. For example, six can be shown as two “threes” on dice; or as the fingers on one hand and one more; or as four and two, using a tens frame.

Teachers should also introduce children to part-whole language (words that describe the relationship between a whole and its parts) and play games that involve partitioning and recombining sets. For example, throw six beanbags, aiming for a hoop. How many go in and how many don’t?

Year 1: Making tens and ones

In Year 1, pupils will need to continue to represent numbers using objects and extend this to pictorial representations. They should build on their understanding of numbers to 10 and be supported to see numbers between 10 and 20 as “10 and a bit more”, using towers of coloured cubes and tens frames.

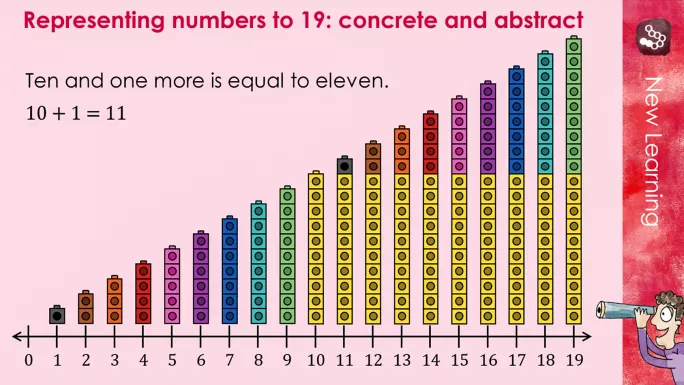
Pupils should be encouraged to begin to recognise place value in numbers beyond 20 by reading, writing, counting and comparing numbers up to 100, supported by manipulatives that can be physically grouped into tens by pupils. This may include cubes and bead strings, as well as real-life objects such as pencils and straws, which can be bundled together with an elastic band.

At this point, we wouldn’t recommend using Dienes ten-blocks (physical blocks that represent 10 units). This is because a Dienes ten-block is fixed and cannot be physically broken into ones. Using objects that can be physically combined together to make a group of 10 will help to focus understanding on the tens and ones relationship.

A pre-grouped 10 (such as a Dienes ten-block) should only be introduced once children are secure in their understanding that 10 ones is equal to one 10.

Year 2: composition of two-digit numbers

1. Everyday objects first, then physical representations

In Year 2, pupils should develop their conceptual understanding of our abstract number system by continuing to practise organising everyday objects into groups of 10, before working with bead strings and Dienes blocks on a place value chart.

2. Connecting the abstract to the pictorial, to the concrete

Pupils can next begin to recognise the place value of each digit in any two-digit number and make connections across pictorial, concrete (Dienes blocks and bead strings) and abstract (numeral) representations. They should be shown that 34, for example, can be composed either of 34 ones, or of three tens and four ones.

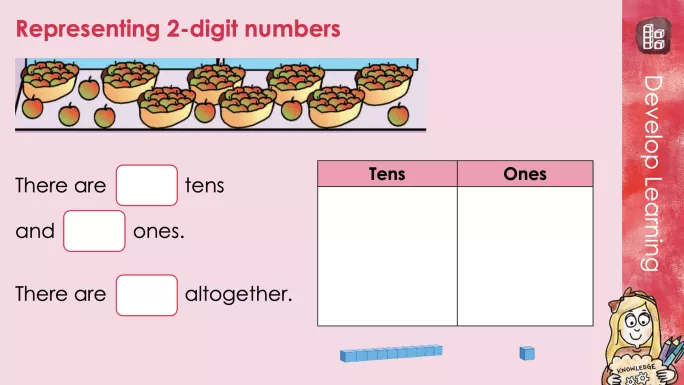
3. Modelling part-whole language

Part-whole language should be modelled to make connections to place value. For example, “34 is my whole, 30 is one part and four is the other part”. And links to commutativity - the fact that changing the order of the parts does not affect the value of the whole - should also be modelled.

Read more:

• Why primary maths needs to be more “phonics”
• What would “phonics for maths” actually look like?
• Five steps to teaching times tables

Years 3 and 4: Representing three- and four-digit numbers

Pupils should next progress to representing numbers with three and four digits.

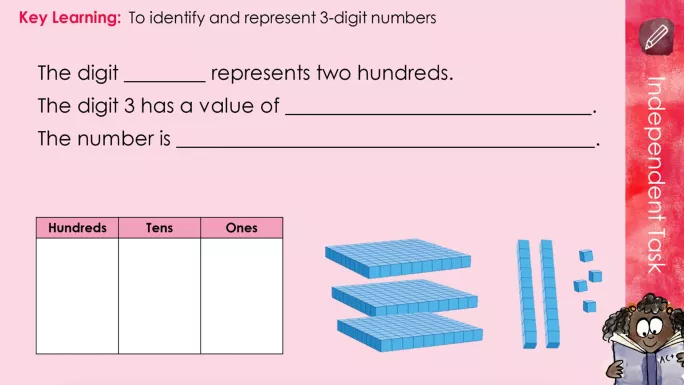
Place value counters shouldn’t be introduced until later in Year 3, once pupils are secure with Dienes. This is because Dienes are different sizes, with 10 “ones” cubes being equal in size to one “tens” block, whereas a place value counter representing one is the same size as a place value counter representing 10.

Dienes blocks allow pupils to visualise the relative magnitude of each digit within a number. Once confident with this, they can progress to using place value counters to explore how the position of a digit affects its value.

Year 5: Representing five-digit numbers and beyond

In Year 5, pupils can start to represent numbers up to 1,000,000 in a variety of ways, including with place value counters and in words, applying their knowledge from earlier year groups.

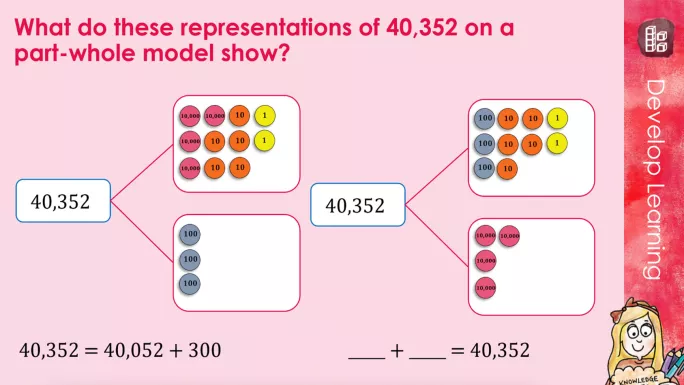
At this point, it’s important to discuss the language of zero as a “placeholder”.

For example, pupils are told that there are “no thousands” in the number 30,003 - but when you say this number out loud, it has thirty “thousands”.

To avoid confusion, explain that the zero in the “thousands” position is “holding the place”, so that the digit three at the front of the number has a value of three “ten thousands” rather than three “tens”, “hundreds” or “thousands”.

Year 6: Representing numbers up to 10,000,000

In Year 6, pupils determine the value of each digit in numbers up to 10,000,000.

It’s helpful to return to the principles of Dienes blocks, as building representations of larger integers supports understanding of the magnitude and relationships between these values.

You can make different representations of 1,000,000 cubic centimetres using cardboard boxes, newspaper or any other resources at hand.

Ultimately, manipulatives and representations are valuable aids in teaching mathematics - but only when they are employed with a clear rationale.

It’s not enough to simply have these tools in front of pupils; teachers need to think explicitly about how to integrate them into lessons and use them to connect learning across year groups.

That’s why understanding place value - and Sats success - has to start in the early years.

Ravi Mohindru is design lead for Mathematics Mastery Primary at Ark Curriculum Plus

For the latest research, pedagogy and practical classroom advice delivered directly to your inbox every week, sign up to our Teaching Essentials newsletter