55Uploads
32k+Views
24k+Downloads
All resources

Statistical significance - t-test: Higher Applications of Maths
Worksheet and datasets for performing paired and independent t-tests on.
All bar one of the datasets are based on real life sources.

Correlation and causation: Higher Applications of Maths
A task which involves generating scatterplots and correlation coefficients using nutritional information from a McDonalds menu.
Worksheet and csv dataset.
Points of interest:
Menu is from America leading to a discussion about how useful is it for use in UK
High number of breakfast items and low number of burgers doesn’t reflect common perception of McD’s menu
Sodium (ie salt) and calories have a strong correlation but this is a spurious relationship (salt has no calories) with portion size being a possible confounding variable

Pearson correlation coefficient tasks: Higher Applications of Maths
Two tasks:
One calculating the Pearson correlation coefficient by hand. A right pain in the backside and shows why we use computers to do such a thing (worth noting doing this by hand is something that could be assessed if doing Level 6 Numeracy).
One getting pupils used to coding the correlation coefficient using statistical software (using the attached csv dataset) and seeing what it means in terms of the regression line without context getting in the way.

Statistical significance - z-test: Higher Applications of Maths
Excuse the emotional whiplash of going from heights of sportsmen to the biggest maritime disasters in history but a few questions on performing z-tests. Includes a dataset to draw figures from for the sportmen question.

Solving Trigonometric Equations With Graphs
First handful of questions have pupils solving trigonometric equations by sketching graphs to identify which quadrants solutions lie in and using the symmetry of said graphs to find the value of these solutions. The second half of the task changes the problems to have pupils working back from a graph or solution to create the equations for themselves.
EDIT: There are a couple of errors on the last page of the answer file.

Special numbers worksheet (square, triangular, Fibonacci, Pascal)
A set of tasks for pupils to pick and chose from working with square numbers, triangular numbers, Fibonacci numbers, and Pascal’s triangle.
Some made up by me, some from various sources credited in the pdf attached.

Thinking about averages and spread using towers
This task focuses on what the averages look like rather than how to calculate them. This could be done with piles of blocks/cubes if you wish (though some of the means work out with decimal values).
Inspired by the “mean average equal sharing” activity by Don Steward:
Resources uploaded:
PDF of resource
Editable Excel spreadsheet of resource
Don Sterward slides from above link

Plotting quadratic graphs - increasingly difficult questions
Answers included if you follow the link included on the last page to the Desmos graphing website.
Inspired by Dave Taylor’s excellent set of resources on his Increasinly Difficult Questions website.

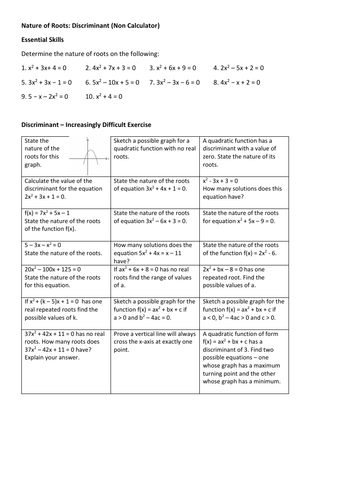
The Discriminant - Increasingly Difficult Exercise
An increasingly difficult exercise on the nature of the roots of quadratics which can be solved with the skills taught at National 5 (though moves beyond the style of question the SQA would ask).
Inspired by Dave Taylor’s Increasingly Difficult Questions website.
Also included are a set of “basic” essential skills questions too (taken from the Free National 5 Maths website).

Scatterplots, correlation, interpretting parameters in bee colonies: Higher Applications
Question sheet and four datasets for use with appropriate statistical software.
Adapted from a Don Steward task about bee colonies.
Each question asks pupils to:
plot a scatterplot
calculate and interpret the correlation coefficient
find the equation of the regression line
interpret one or both of the equation parameters
make a prediction using the regression line

Graphing continuous data (Spotify playlist data): Higher Applications of Maths
Pupils use histograms and boxplots to illustrate various continuous numerical variables in RStudio using a csv dataset.
Variables are values Spotify uses to categorise songs. Songs in the dataset and taken from a playlist.
A bit of fun included asking pupils to pick some songs that would suit the tastes of the person who created the playlist (me!). If you use this and pupils make suggestions let me know on Twitter at @bucksburnmaths.
To give pupils an idea of what tempo feels like I play them Juice by Lizzo which is 120 bpm. Also played them You Suffer by Napalm Death (1.3 seconds long) and Mogwai Fear Satan by Mogwai (16 minutes long) as a way of talking about outliers. Plus, any excuse to talk about the 1980s grindcore scene!

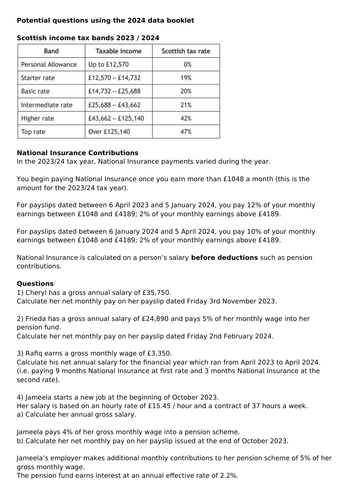
Higher Applications of Maths - varying National Insurance rates
A handful of questions based on the National Insurance rates given in the 2024 data booklet.

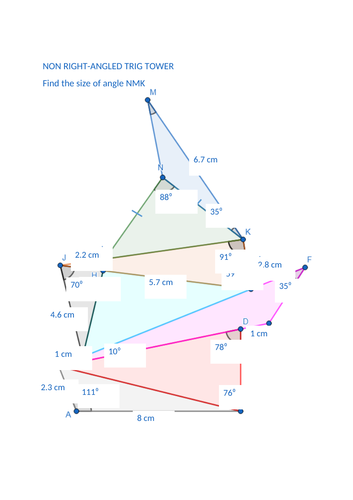
Sine and Cosine rule trigonometry pile up
Work from the bottom to get an answer at the top!
No “ambiguoius” cases (where you need to use sin(x)=sin(180-x)).
Solutions will be uploaded eventually!

Increasingly Difficult Exercise: Equation of a Cirlce (SQA Higher Maths)
An set of questions that gets increasingly difficult with each subsequent question. Covers course content for SQA (Scottish) Higher. This task was uploaded to Chris McGrane’s starting points website a few years back. I’ve uploaded it here with a handwritten set of solutions.

Optimization - scaffolded problems
Something pupils traditionally find difficult. All context stripped away and problems laid out in a structured grid. Handwritten solutions included.