How to save teachers 5 million hours a year (without affecting learning)

This article was originally published on 14 May 2024.

Many schools regularly collect, and then centrally deposit, test data with the aim of tracking pupil progress and planning “interventions” for students who are falling behind.

Indeed, Teacher Tapp data from 2023 shows that 36 per cent of (7,674) respondents work in schools that do this half termly or more and 88 per cent of respondents work in schools that do this termly or more.

Last year, FFT Datalab wrote a blog using data on hundreds of thousands of termly tests to look at the variation in standardised scores from one term to the next. How much would we expect a primary pupil’s maths score to change from autumn to spring term, for example?

Most pupils move very little. On a scale where two-thirds of pupils score between 85 and 115, half of pupils’ spring term scores are within five points of their autumn term scores. But some pupils show more change. Just under a third of pupils’ spring term scores are 5 to 10 points away from their autumn term scores.

This data allows us to ask a second interesting question: how many pupils change their score enough that a test can reliably detect that change?

Measurements can only ever be accurate to a certain extent. If I asked three people to measure my height in millimetres, for example, I would get three slightly different answers. The difference reflects measurement error. This is somewhat random in nature - some measurements would be too high and others too low.

• The 23 tasks teachers shouldn’t do
• Revealed: How schools are trying to cut teacher workload
• Schools wanted for ChatGPT teacher workload trial

Pupil test scores also contain measurement errors. And owing to a recent Education Endowment Foundation review, we now know more about the size of measurement error in some commercially available tests. This allows us to say some useful things about the smallest change in pupil test scores that we can detect with a given level of confidence.

Keep in mind the analogy with measuring height here. If my 16-year-old cousin measured 165cm in 2023 and 175cm in 2024, we could be pretty confident that they had genuinely grown. But if they measured 165cm in 2024 and 165.1cm in 2025, we couldn’t confidently rule out that the change was just pure measurement error.

Based on the information in the EEF review, it turns out that carefully designed tests can, with 90 per cent confidence, detect a change in standardised test scores of about 13 or more. So, how often do pupils make a change of 13 or more?

The chart below shows changes from autumn to spring (top panel), spring to summer (middle panel) and across two terms from autumn to summer (bottom panel). The pink lines show changes greater than 13 points (up or down). Interventions are usually focused on those whose scores have fallen, which makes the left-hand pink line the relevant one.

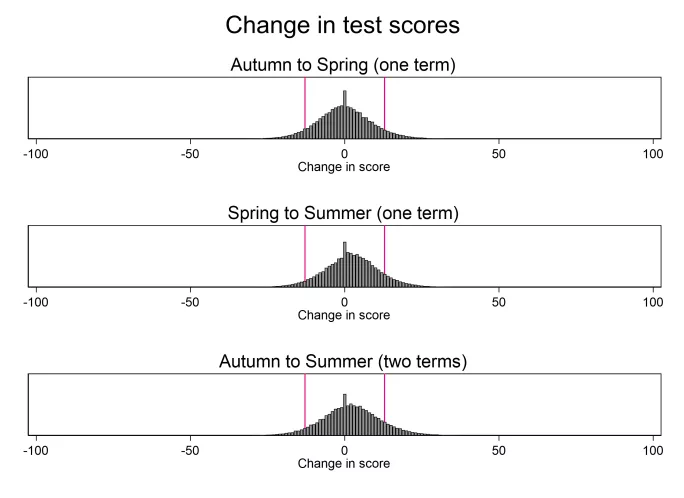
What’s notable from the graphs is how few pupils we can conclude (with 90 per cent confidence) have changed their score at all. When we look at the change across one term (the top two graphs), only about one in 20 (5 to 7 per cent) see a fall in test scores that can be detected with a well-designed test. When we look at change across two terms (bottom graph), this remains essentially unchanged at 6 per cent.

For pupils who make smaller changes from one term to the next, we can be correspondingly less confident that they have changed at all. Half of pupils change by five points or less from one term to the next. We can be less than 50 per cent confident (worse than a coin flip) that this is not just pure measurement error.

A third of pupils change by 5 to 10 points from one term to the next. We can be 50 to 80 per cent confident (a little better than a coin flip) that this is not just pure measurement error.

For a number of reasons, the situation is likely to be worse than this in most schools. First, the above analysis is based on the precision of a carefully designed test developed by assessment experts, but most schools use less precise tests that have been developed in-house.

Second, the above analysis is based on the precision of a science test, but most subjects are harder to assess than science.

Third, the above analysis is based on the precision of tests for the average-scoring students, but most students do not get the average score and tests become less precise for pupils who are further from the mean. I suspect the proportion of pupils for whom we can conclude (with 90 per cent confidence) that their score has declined from one term to the next is closer to 0 per cent than it is to 5 to 7 per cent.

This does not mean these tests are uninformative. Averaging across the pupils in a group helps to cancel out the measurement error. The test scores might be useful for school leaders looking to understand progress in a given subject or cohort. But when it comes to capturing pupil-level change from one term to the next, termly testing is only informative for a small minority of pupils.

Data drops and teacher workload

The above matters because data drops generate additional work for teachers and England has a problem with workload. In the Teaching and Learning International Survey 2018 data, teachers in England have some of the highest working hours among all participating countries.

Also in 2018, the government’s Making Data Work report stated: “We have not encountered any examples of schools where the actions arising after a half-termly deposit of attainment data justify the time investment required by teachers to facilitate six data collection points a year.

“Unless attainment information can be collected with no marking or data inputting time outside teachers’ lesson times, we see no reason why a school should have more than two or three attainment data collection points a year, which should be used to inform clear actions.”

In the subsequent five years, the proportion of Teacher Tapp respondents working in schools doing half-termly data drops fell from 56 per cent to 36 per cent. I suspect that leaders in the remaining third believe that the particular/special way in which they do it in their school does justify the time required.

However, based on the new information we have gained since 2018 (see part 1, above), it is pretty clear that half-termly data drops are not justified because, for 95 per cent or more of pupils, we can’t confidently distinguish a fall in their test score from pure measurement error. We have been allocating pupils to “interventions” based largely on random noise.

If this still feels counterintuitive, remember the analogy with height. Trying to measure change in height over 48 hours isn’t a sensible thing to do because the expected change is dwarfed by the measurement error.

This is good news. It means we can cut teachers’ workload without any material risk of harming students’ education.

We can still regularly test pupils, which is great for learning. But the time-consuming marking, data entry, meeting cycles and targeted intervention planning can all be done away with.

How much workload could we save? We can do some back-of-the-envelope calculations to get a sense of this.

I conducted a not-very-scientific Twitter/X poll to understand how many hours of workload are involved per data drop, per teacher.

The median response seems to be about three hours. When I have shown these results to teachers, they have suggested that this looks on the low side. But let’s adopt this as a possibly conservative assumption.

Let’s start by considering a scenario in which all schools move to doing no more than termly (three per year) data drops. For the sake of argument, let’s assume the 36 per cent of Teacher Tapp respondents who report doing half-termly data drops are spread equally across these schools and the schools are of approximately equal sizes.

There are 567,309 teachers in England, meaning that approximately 204,231 (36 per cent) are doing half-termly data drops. Reducing this to termly would save three (data drops) multiplied by three (hours per data drop), or 1.83 million hours of workload system-wide. This amounts to just over one working day (nine hours) per year for each teacher in these schools. The case for making this change is very strong.

Having said that, I am doubtful that termly data drops are justified. They are not helpful for targeting interventions at struggling pupils because the data on which they are based consists largely of measurement error/random noise.

Based on conversations that I have had with experienced headteachers, I am also doubtful that termly data drops are helpful for school leaders. What kind of subject-wide or cohort-wide changes would leaders actually implement on a term-to-term basis in response to this data? You wouldn’t change the curriculum every term or change the leadership of the maths department every term. At the end of an academic year, maybe, but not termly.

On the basis that there is no point in collecting data you would not act on, let’s consider a scenario in which all schools move to doing one data drop per year. That means that 204,231 teachers would drop from six per year to one per year, collectively saving 3.06 million hours per year. Again, based on Teacher Tapp data, a further 295,000 (52 per cent) of teachers do between three and five data drops per year. Let’s assume they are all doing three per year and would drop to one. This would collectively save 1.77 million hours per year.

Finally, Teacher Tapp suggests that another 39,711 (7 per cent) are doing two data drops per year and these would now drop down to one. Collectively, they would save another 0.12 million hours per year.

Across all three groups, this amounts to a saving of 4.95 million hours of workload per year, which is just over one day per year (8.7 hours) for every teacher in the country.

Samuel Sims is an education researcher at the UCL Institute of Education and the Education Datalab. This piece was originally published on his blog

For the latest research, pedagogy and practical classroom advice delivered directly to your inbox every week, sign up to ourTeaching Essentials newsletter